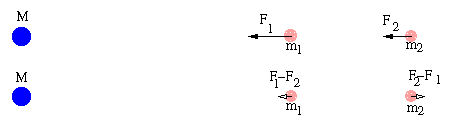Aula anterior
Equação da energia
Considerando um sistema de dois corpos interagindo gravitacionalmente, onde
- m1 e m2 são as massas dos corpos
- v1 e v2 são suas velocidades
- r é a distância entre ele
Conservação da energia no movimento orbital:
Chamando W o trabalho realizado pela força gravitacional sobre um
corpo que se move entre dois pontos A e B:
WAB = ∫AB F.dx
onde dx é um elemento infinitesimal da trajetória.
Para calcular o valor dessa equação, observamos que:
F.dx= m . dvdt . vdt = m(v.dv) = d(mv2/2)
A equação do trabalho fica:
WAB = ∫AB F.dx= ∫AB d(mv2/2)
= (mv2/2)B - (mv2/2)A = ECB- ECA
onde EC = energia cinética.
Por outro lado, como a força que está atuando é a força gravitacional entre dois corpos m1 e m2, temos que:
F.dx= - G m1 m2/r2. dr = d( G m1 m2/r)
e a equação do trabalho fica:
W = (G m1 m2/r)B - (G m1 m2/r)A = EPA - EPB
onde EP = energia potencial = Gm1 m2/r
Combinando as duas equações do trabalho encontradas:
ECB- ECA = EPA - EPB
ECB+ EPB = ECA + EPA
E chamando E = EC + EP = Energia total do sistema
E
A =E
B = constante
Sabendo que a energia total se conserva nesse sistema,
|
Energia total = 1⁄2(m1v12) + 1⁄2(m2v22) - Gm1m2 ⁄ r = constante
|
Da conservação do momentum linear total:
m1v1=m2v2 (onde assumimos momentum linear total = 0)
Então:
v1=m2v2/m1 e
v2=m1v1/m2 (1)
Definindo
v= velocidade relativa=v1+v2
Podemos escrever:
v1=v - v2 e v2=v - v1 (2)
Substituindo (2) em (1) podemos escrever:
v1=[m2/(m1+m2)]v e v2=[m1/(m1+m2)]v
Substituindo na equação da energia total:
Energia total = m1m2/(m1+m2)[v²/2 - G(m1+m2)/r]
Calculando o valor da energia total no periélio, onde
r = a(1-e) e v2 = 4π2a2/P2[(1+e)/(1-e)]
e lembrando que P2 = [4π2/G(m1+m2)]a3
Encontramos que a energia total vale:
E a equação da energia fica:
|
v² = G (m1+m2)[2/r - 1/a] |
Casos especiais:
- Velocidade para órbita circular:
Na órbita circular a = r, e substituindo na equação da velocidade temos:
v²circ = G (m1+m2)[2/r - 1/r] = G (m1+m2)/r →
Para uma órbita circular, a energia total é negativa, já que:
- Velocidade para órbita parabólica:
Na órbita parabólica a = ∞, substituindo na equação da velocidade temos:
v²esc = G (m1+m2)[2/r - 1/∞] = 2G(m1+m2)/r →
Para uma órbita parabólica, a energia total é nula, pois:
Veja mais exercícios simples sobre gravitação em: http://www.fisicalega.net/exercicios/gravitacao/gravitacao2.html
Forças gravitacionais diferenciais ou Forças de maré
texto completo artigo do prof. Lang sobre marés
Forças gravitacionais diferenciais
São forças que surgem dentro de um corpo extenso que esteja no campo
gravitacional de outro.
Chamando
- F a força que atua no centro de massa do corpo extenso
- e r a distância do centro de massa ao outro corpo
Cada partícula do corpo extenso está a uma distância (r+dr)
ao outro
corpo, e portanto sente uma força gravitacional (F + dF).
A diferença de força dF entre dois pontos separados por uma distância dr
vale: dF = (2GMm)/(r3) dr (veja a dedução aqui).
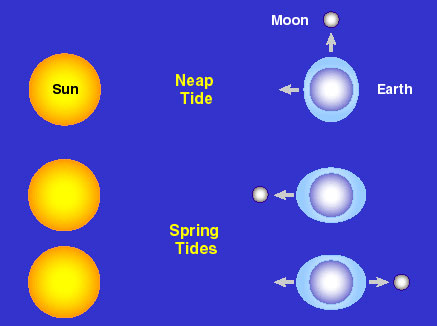
Marés
Causas:
forças gr avitacionais diferenciais exercida pela Lua e pelo Sol sobre a Terra
Idéia básica:
O puxão gravitacional sentido pelas partículas no lado mais próximo da Lua é maior do que puxão gravitacional sentido pelas partículas no centro que é maior do que puxão gravitacional sentido pelas partículas no lado mais distante da Lua. Portanto,
Em relação
ao centro da Terra, um lado está sendo puxado
na direção da Lua e o outro lado está sendo puxado na direção
contrária.
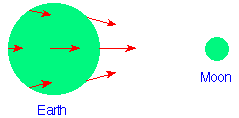
Figura fora de escala da Terra e da Lua
as marés acontecem duas vezes a cada
24h 48min, que é a duração do dia lunar.
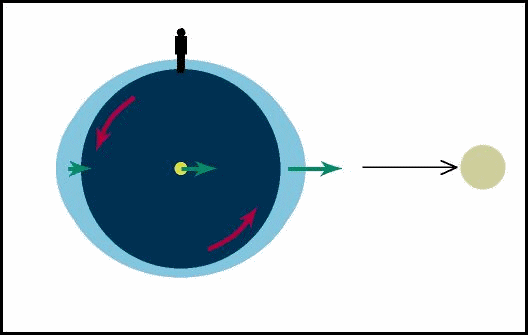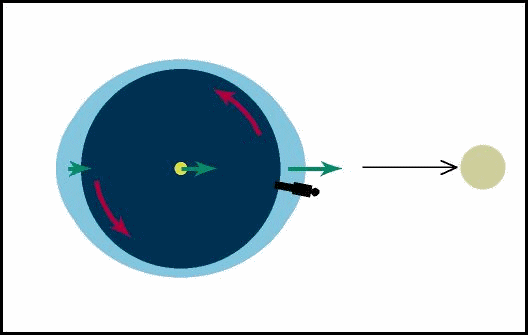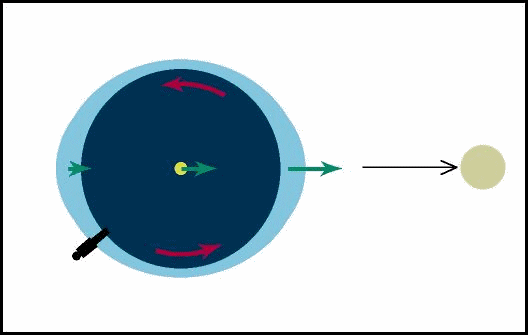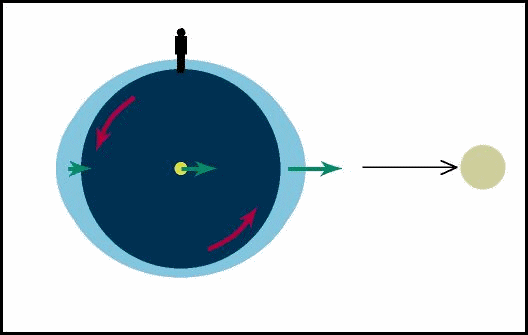
Figura fora de escala da Terra e da Lua
Diário de classe