Sabemos que um dia solar médio tem 24h solares de duração, cada hora solar dividida em 60 minutos (solares) e 3600 segundos (solares). Estes são os intervalos de tempo usados em nossa vida cotidiana. Expresso nessas unidades, o dia sideral tem uma duração de 23h56m04.090538s. Mas podemos definir intervalos como hora, minuto e segundo siderais, de forma que o dia sideral tenha 24h siderais. Claro que a unidade de tempo sideral necessariamente será sempre mais curta do que a unidade solar. Uma questão importante e recorrente em determinações astronômicas é a de como converter intervalos de tempo expressos em unidades siderais em solares ou vice versa.
Suponha que tenhamos um intervalo ΔS de tempo sideral. Queremos saber qual o valor ΔM deste mesmo intervalo em unidades de tempo solar.
Para melhor entendermos por que o mesmo intervalo tem valor numericamente maior em unidades siderais do que solares médias, basta lembrarmos que o tempo é baseado, em ambos os sistemas, em valores de ângulo horário: do ponto γ (Sol Médio) no caso do sistema sideral (solar médio).

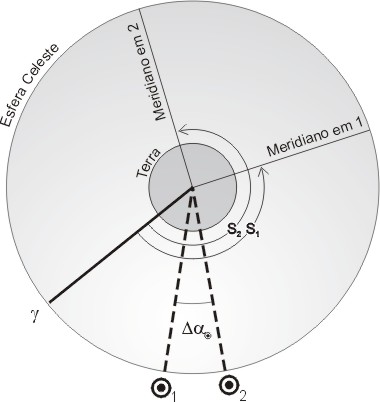
Na figura acima mostramos o intervalo, expresso em unidades siderais, ΔS = S2 - S1 decorrido entre dois instantes no tempo. Neste intervalo, o meridiano de um observador, devido à rotação da Terra, varreu exatamente este ângulo ΔS no espaço. Isso porque o observador é móvel, enquanto o ponto Vernal pode ser considerado como fixo na esfera celeste durante o intervalo. Já a posição do Sol Médio, se deslocará ligeiramente para leste, devido ao movimento anual do Sol. Sua ascensão reta aumentará então por Δα(°) = ΔS(°) / 366.25, onde 366.25 é o número de dias siderais no ano. Assim, o valor do mesmo intervalo em unidade solares médias, ΔM, será menor:
ΔM = ΔS - Δα = ΔS (1 - 1 / 366.25) = ΔS (1 - 0.00273043359) = ΔS (1 - μ)
onde μ = 1/366.25 = 0.00273043359.
O mesmo fator de conversão pode ser obtido lembrando que um dia sideral tem 24h siderais (por definição de hora sideral), mas apenas 23h56m04.090538s solares médios. Logo, temos a regra de proporcionalidade:
ΔS / ΔM = 24h / 23h56m04s = 1.00273790926 = 1 + η
onde η = 0.00273790926. Note que é válida a relação:
(1 + η)(1 - μ) = 1
Assim, se conhecemos a hora sideral em um dado meridiano em um determinado instante, S0, e desejamos conhecer a hora sideral S no mesmo meridiano decorrido um intervalo em hora solar igual a ΔM, teremos:
ΔS / ΔM = 1 + η ---> ΔS = S - S0 = (1 + η) ΔM
S = S0 + (1 + η) ΔM
É comum, por exemplo, querermos conhecer a hora sideral S às M horas solares médias locais em um determinado meridiano de longitude λ. Sabemos que se são M horas solares médias locais nesta longitude, o tempo universal neste instante será TU = (M+λ) (como de hábito adotamos a convenção de que λ > 0° a oeste de Greenwich e λ < 0° a leste de Greenwich. Das efemérides (do ON ou do Astronomical Almanac, por exemplo) podemos ler a hora sideral S0 em Greenwich correspondente a TU=0h para o dia em questão. Em unidades solares médias, ter-se-ão decorrido ΔM = (M+λ) horas desde este instante. O intervalo em horas siderais correspondente será, portanto:
ΔS = ΔM (1 + η) = (M + λ) (1 + η)
A hora sideral em Greenwich, SG, no instante desejado será portanto:
SG = S0 + ΔS = S0 + (M+λ)(1+η)
Mas queremos a hora sideral S no meridiano de longitude λ e não em Greenwich (λ = 0°). Precisamos então subtrair a diferença em longitude:
S = SG - λ = S0 + (M+λ)(1+η) - λ = S0 + (M+λ)η + M; eq. (1)
A expressão acima nos dá exatamente o que queríamos: a hora sideral em um meridiano de longitude λ dada e no instante em que a hora solar média local é M. Como já mencionado, o valor de S0, a hora sideral em Greenwich (λ = 0°) à TU=0h é listada, dia a dia no ano, no Anuário Astronômico do Observatório Nacional (ON) ou no Astronomical Almanac.
Exemplo de tabela do Anuário do ON com valores de S0
Exemplo de tabela do Astronomical Almanac com valores de S0
A fórmula acima é bastante geral. Suponha que queiramos simplesmente a hora sideral em Greenwich a uma hora solar média local M. Como se trata do meridiano de Greenwich, a hora solar média local é também a hora universal: TU = M. Além disso, λ = 0h. Logo, a hora sideral desejada será:
S = S0 + M (1+η) = S0 + TU (1+η)
onde S0 é a hora sideral em Greenwich à 0h TU (que pode ser encontrada em Efemérides) e η = 0.00273790926.
Outro exemplo: provar que a hora sideral S em um meridiano de longitude λ à M=0h solar média local é dada por:
S = S0 + λη
onde, como sempre, S0 é a hora sideral em Greenwich a TU = 0h.
Consideremos ainda uma situação, bastante comum, em que temos que escolher uma estrela para observação em um determinado dia e intervalo de hora legal. A ocasião mais favorável para observarmos uma estrela é, em geral, próxima do instante de sua culminação superior, quando sua altura no céu é máxima. Suponha que tenhamos o intervalo de hora legal compreendido entre HL1 e HL2 (HL2 > HL1) para a observação. Inicialmente temos que converter hora legal HL em hora solar média local M. Como vimos, a diferença entre as duas será igual à diferença entre a nossa longitude, λ, e a longitude do meridiano central do fuso horário em que nos encontramos, λc.
M1 - HL1 = λc - λ ====>>> M1 = HL1 + λc - λ
M2 - HL2 = λc - λ ====>>> M2 = HL2 + λc - λ
Os valores de hora sideral S1 e S2, correspondentes, respectivamente, a M1 e M2, serão dados pelas expressão (1) acima, sendo que o valor de S0 , a hora sideral em Greenwich à TU=0h, é sempre tirado das efemérides. Como sabemos que a culminação de uma estrela ocorre à hora sideral igual à sua ascensão reta, α, temos que escolher nosso alvo usando o critério em ascensão reta S1 < α < S2.
Suponha agora que queiramos fazer o inverso: determinar a hora solar média local, M, dada a hora sideral S num dado instante. Basta resolvermos a equação (1) acima para M:
M = (S - S0 - λη)/(1+η).
Como (1 - μ) = 1/(1 + η),
M = (S - S0 - λη) (1-μ)
onde μ =0.00273043359.
Basilio Santiago, santiago@if.ufrgs.br