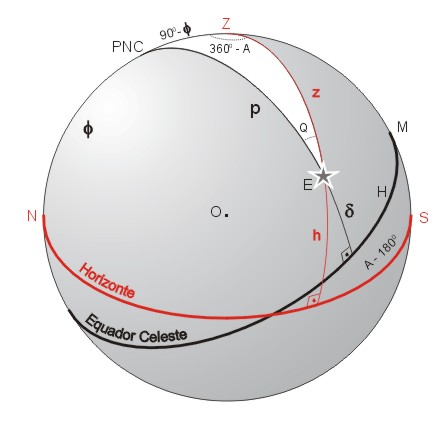
Apliquemos agora as fórmulas de Trigonometria Esférica deduzidas anteriormente ao triângulo de posição de uma estrela, representado na figura abaixo pelo triângulo esférico E-Z-PNC. Os lados deste triângulo, conforme indicado, são o complemento da latitude do observador (90° - φ), a distância zenital z (= 90° - h) e a distância polar p (= 90° - δ). Além do ângulo Q, com vértice em E e mostrado na figura, ou outros ângulos do triângulo de posição são o ângulo horário H, com vértice em PNC (pois é o ângulo entre o plano meridiano NZMS e o círculo horário da estrela, que liga E a PNC) e 360° - A, com vértice no zênite. Este último é o ângulo entre o plano meridiano (NZMS) e o vertical da estrela (que liga E a Z), estando obviamente ligado ao azimute. O fato de seu valor ser 360° - A se deve à escolha particular da origem do azimute na direção norte e crescendo para leste-sul-oeste.
A analogia dos senos nos dá então:
cos δ / sen (360° - A) = cos φ / sen Q = sen z / sen H ==>>
Note que na simplificação da analogia dos senos feita acima, utilizamos propriedades conhecidas do seno de uma soma. Aliás, o leitor já deve ter notado que o estudo da Astronomia Esférica exige bastante familiaridade com a Trigonometria Plana, que é estudada no Ensino Básico.

Já as fórmulas dos 4 elementos nos dão:
Essas fórmulas, dos senos e dos 4-elementos, são extremamente úteis e, em geral, suficientes, para o estudo analítico do movimento diurno das estrelas. Elas têm validade geral, para qualquer estrela, qualquer instante (note que o tempo entra explicitamente nestas equações através do ângulo horário H) e para qualquer observador (a posição do observador entra explicitamente pela sua latitude φ).
Existem algumas situações especiais nas quais as fórmulas deduzidas acima se simplificam bastante. Essas situações se caracterizam pelo fato de um ou mais dos lados ou ângulos do triângulo de posição se tornarem nulos ou retos.
A situação mais simples é a da passagem meridiana. Neste caso o ângulo horário é H = 0°. Pela analogia dos senos vê-se imediatamente que os senos dos demais ângulos do triângulo de posição também têm que se anular, ou seja, o azimute por exemplo assume os valores A = 0° ou A = 180°. Estes dois casos se aplicam a culminações a norte e a sul do zênite, respectivamente. É fácil ver também, pela primeira fórmula dos 4 elementos acima, que:
cos z = sen δ sen φ + cos δ cos φ = cos (δ - φ) ==>> z = +/-(δ - φ).
Essas expressões já haviam sido deduzidas no capítulo sobre o movimento diurno, usando diagramas do plano meridiano. O sinal positivo acima vale para estrelas que culminame entre o zênite Z e o ponto cardeal norte (N), ou seja, com azimute na culminação A = 0°. Já o sinal negativo vale para culminações que se dão a sul do zênite (A = 180°). O leitor cuidadoso e metódico vai notar que as mesmas relações deveriam ser também obtidas no caso da culminação inferior, quando H = 180°. Mas, de fato, se fizermos esta substituição nas equações deduzidas acima, teremos:
cos z = sen δ sen φ - cos δ cos φ = - cos (δ + φ) ==>> z = 180° - δ - φ
O problema com o caso acima é que H = 180° corresponde ao instante da culminação inferior e não da superior. Na culminação inferior a altura da estrela é mínima (distância ao zênite é máxima). Se você desenhar o diagrama do plano meridiano e tentar deduzir a relação entre z, δ e φ para o caso em que a estrela está em culminação inferior, é justamente esta fórmula que será obtida, demonstrando assim a inteira aplicabilidade das relações da Trigonometria Esférica aos casos de passagem meridiana.
Outra situação especial que se simplifica as relações entre as coordenadas é o nascer e ocaso de uma estrela, quando z = 90°. Neste caso, pela fórmulas dos 4 elementos que envolve o ângulo horário H, temos:
A primeira expressão acima, mostra que um astro só nasce e se põe se |tg δ tg φ| < 1 -->> |tg δ| < |cotg φ| -->> |tg δ| < |tg (90°-φ)| -->> |δ| < |90°-φ|
A segunda expressão resulta na mesma restrição acima, pois |cos A| também tem que ser menor do que a unidade
A restrição obtida acima requer cuidado de interpretação. Se a latitude é φ < 0, então 90° - φ > 90°, o que viola o domínio de valores permitidos para a declinação δ. Assim, no caso de um observador no hemisfério Sul, podemos substituir (90°-φ) por (90°+φ), já que o módulo da tangente será o mesmo, independente do sinal aritmético do argumento. Usando o sinal positivo no argumento, respeitamos os limites possíveis para a declinação.
Ou seja, uma estrela nasce e se põe somente se
Essas condições também já haviam sido deduzidas anteriormente, quando estudamos estrelas circumpolares e invisíveis.
Há ainda outras situações úteis, em que as fórmulas da Trigonometria Esférica se simplificam. Por exemplo, quando A = 90° ou A = 270° dizemos que a estrela passa pelo 1° e 2° verticais, respectivamente. Analogamente, quando H = 90° ou H= 270°, temos os círculos das 6 e 18 horas. Quando Q = +/- 90°, dizemos que a estrela está em elongação. Em todas estas situações o triângulo de posição da estrela é retângulo. Há outras situações em que o triângulo de posição se torna retilátero, ou seja, com um lado igual a 90°. Vimos o caso do nascer e ocaso (z = 0°). Há também os casos que envolvem astros ou observadores especiais, como o de uma estrela que pertença ao Equador Celeste (δ = 0°), ou o de um observador situado no Equador da Terra (φ = 0°). Procure você mesmo deduzir as fórmulas dos senos e dos 4 elementos nestes casos especiais.
Um outro conceito importante é o de velocidade zenital . Esta é a taxa de variação no tempo da distância zenital, dz/dH. Podemos deduzir uma expressão para a velocidade zenital usando a fórmula dos quatro elementos envolvendo o ângulo horário:
Para isto basta derivarmos ambos os lados desta fórmula com relação ao ângulo horário (= tempo). Teremos então:
O valor da velocidade zenital do Sol quando este está próximo do horizonte (z ~ 90°, sen z ~ 1), por exemplo, determina a duração daquela fase do dia em que nem é dia claro nem escuridão total, o que comumente denominamos de crepúsculo ou alvorada, dependendo de ser o entardecer ou o amanhecer. Quanto menor o valor de dz/dH nestas fases do dia, mais tempo elas duram. Pelo fato da velocidade zenital variar com o cosseno da latitude do observador, concluímos que dz/dH tende a ser menor em latitudes mais extremas. Veremos mais adiante que a declinação do Sol está sempre dentro do intervalo (-23.5°, + 23.5°), sendo que os valores extremos ocorrem em junho e dezembro, nos chamados solstícios. Assim, nessas épocas e para observadores de mais alta latitude, o entardecer e o amanhecer se dão mais lentamente.
Basilio Santiago, santiago@if.ufrgs.br