Trigonometria Esférica

Já estudamos qualitativamente o movimento diurno, concluindo que todos os astros completam diariamente um círculo paralelo ao equador celeste. Estudamos o caso particular em que um objeto atravessa o meridiano astronômico de um observador e vimos que nesta situação a sua altura no céu atinge um valor extremo (máximo na culminação superior e mínimo na culminação inferior). Além disso, estabelecemos relações matemáticas entre a latitude do observador e a declinação e altura da estrela na passagem meridiana. Na verdade, as coordenadas de uma estrela no céu estão associadas à posição do observador na superfície da Terra em qualquer instante, mesmo fora da passagem meridiana. Há relações matemáticas bem mais gerais envolvendo coordenadas horizontais, horárias e equatoriais de uma estrela e a latitude e longitude do observador. Para deduzirmos essas relações, contudo, faz-se necessário estudarmos um ramo da Trigonometria chamado de Trigonometria Esférica , cuja aplicação à Astronomia constitui-se no que chamamos de Astronomia Esférica. Esta não é a mais excitante das disciplinas, mas é muito importante para a prática da Astronomia, pois o céu tem geometria esférica e não plana.

A Trigonometria Esférica é análoga à trigonometria plana, mas com a diferença muito importante de ser aplicada a triângulos esféricos.

Triângulos Esféricos

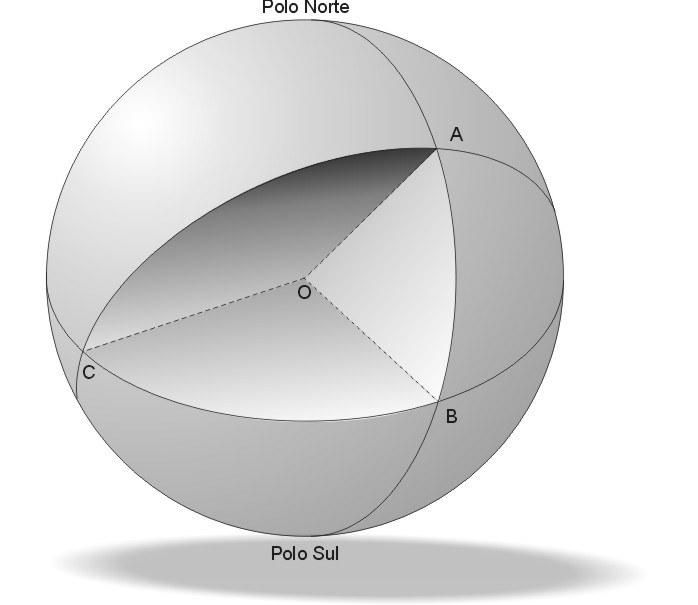
Um triângulo esférico é uma figura sobre uma superfície esférica que resulta quando consideramos 3 grandes círculos (ou círculos máximos) sobre essa superfície. Um grande círculo é qualquer círculo sobre a superfície esférica que a divida em dois hemisférios. Um plano que contém um grande círculo necessariamente contém também o centro da esfera. A figura abaixo mostra um triângulo esférico. Vemos uma esfera com centro em O e três pontos em sua superfície: A, B e C. Ao unirmos estes 3 pontos, dois a dois, através de círculos máximos, formamos um figura ABC que se assemelha a um triângulo, mas que se situa sobre a esfera: um triângulo esférico portanto.

Note que um triângulo esférico não é qualquer figura de três vértices desenhada sobre uma esfera; para ser um triângulo esférico esta figura tem que ter lados que sejam arcos de grande círculo. Outra observação importante sobre triângulos esféricos é que tanto os seus ângulos quanto os seus lados são medidos em unidades angulares. Os lados de um triângulo esférico são arcos de círculo máximo que, divididos pelo raio da esfera nos dão o ângulo entre os pontos que ligam. Já os ângulos em cada vértice do triângulo esférico representam a separação angular entre os planos dos grandes círculos que se interceptam naquele vértice.

Os triângulos esféricos têm algumas características que os distinguem dos planos. Neste últimos, por exemplo, a soma dos seus ângulos internos é sempre igual a 180°. No caso dos esféricos, a soma dos ângulos é sempre compreendida entre 180° e 540°. Existem vários livros que abordam a Trigonometria Esférica de uma perspectiva mais geral e aprofundada, discutindo e apresentando vários teoremas e resultados de interesse geral sobre os triângulos esféricos. Aqui vamos adotar uma abordagem mais objetiva, voltando-nos diretamente para situações de interesse Geodésico e Astronômico.

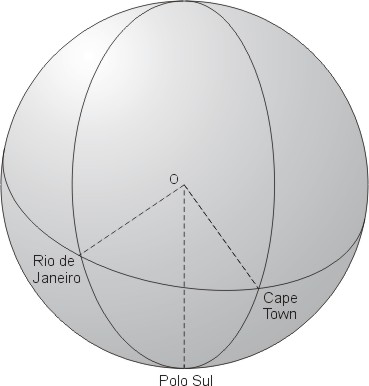
Na figura abaixo vemos um exemplo geográfico de um triângulo esférico. Trata-se do triângulo que tem como vértices o pólo sul geográfico e as cidades de Rio de Janeiro e Cape Town (África do Sul). Os lados do triângulo que ligam cada uma dessas duas cidades ao pólo Sul são simplesmente arcos ao longo dos seus respectivos meridianos geográficos (arcos de grandes círculos portanto). Já o lado que liga as duas cidades é também um arco de grande círculo.

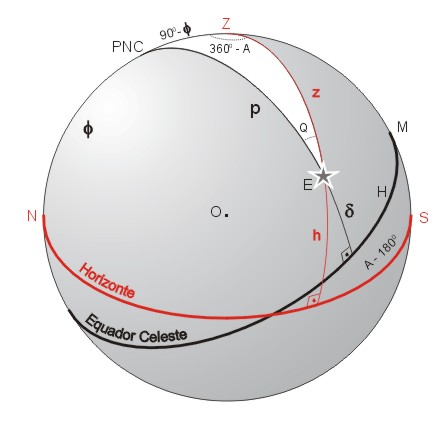
Por que o estudo de triângulos esféricos é importante para a Astronomia? O motivo é que, em qualquer instante, exceto pela passagem meridiana, um astro forma com o pólo celeste de seu hemisfério equatorial e com o zênite um triângulo esférico. Este triângulo é chamado de triângulo de posição do astro. Na figura abaixo vemos representado o triângulo de posição de uma estrela (cuja posição na esfera celeste é representada pela letra E). A figura abaixo inclui também a posição do observador (O), os planos equatorial e horizontal e o plano meridiano (contendo N, Z, M e S). Estão indicadas na figura várias coordenadas associadas à estrela, como sua altura h, sua distância zenital z, sua declinação δ e sua distância polar p. Estão indicados ainda o ângulo horário H da estrela e, pela altura do pólo celeste elevado (PNC), a latitude φ do observador.

Fórmulas de Trigonometria Esférica

Podemos então aplicar inúmeras relações entre os elementos de um triângulo esférico ao triângulo de posição de um astro. Estas relações são deduzidas a seguir para um triângulo esférico genérico, de lados a, b e c e ângulos A, B e C. Na próxima seção, aplicaremos as fórmulas aqui deduzidas ao triângulo de posição de uma estrela. Considere o triângulo genérico abaixo, mostrado em tonalidade cinza. Na figura também mostramos o centro da esfera, O. Conforme já mencionado, o lado a do triângulo, por exemplo, é um arco de grande círculo que mede o ângulo entre os segmentos de reta OC e OB, e assim por diante. Ele é o lado oposto ao vértice que têm ângulo A. Este ângulo, por seu turno, mede a separação entre os planos OAB e OAC.

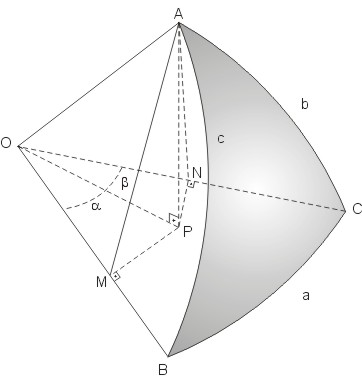
Vamos agora deduzir algumas fórmulas importantes que associam lados e ângulos de um triângulo esférico. Primeiramente, consideremos a perpendicular ao plano OBC e que passa pelo vértice em A do triângulo da figura acima. Essa reta é representada pelo segmento AP da figura. A partir do ponto P, tomemos agora duas retas, PM e PN, perpendiculares, respectivamente, ao segmentos OB e OC. Ao tomarmos estas retas, formamos na figura vários triângulos (planos) retângulos: APN, APM, ONP, OMP e OPA. Em cada um deles, o ângulo reto está no vértice no meio do nome do triângulo (exemplo: o triângulo APN é retângulo no vértice em P). Além desses, são também triângulos retângulos ONA e OMA. Usando todos estes triângulos poderemos então deduzir várias fórmulas.

Considere o triângulo ONA, por exemplo. O ângulo com vértice em O deste triângulo mede as separação entre o cateto ON e a hipotenusa OA. Mas este ângulo é o lado b do triângulo esférico. Logo podemos escrever:

cos b = ON / OA ; sen b = AN / OA

Analogamente, considerando o triângulo OMA, cuja hipotenusa é OA (o raio da esfera), teremos:

cos c = OM / OA ; sen c = AM / OA

Sejam agora os triângulos OMP e ONP, cuja hipotenusa é OP. E sejam novamente os ângulos com vértice em O, representados pelas letras gregas α e β. Podemos escrever:

cos α = OM / OP ; cos β = ON / OP

Podemos então escrever que OM = OP cos α. Substituindo esta relação na expressão para cos c acima e lembrando que α + β = a, temos:

OM = OA cos c = OP cos (a-β) = OP (cos a cos β + sen a sen β) ==>>

==>>OA cos c = OP (cos a ON/OP + sen a NP/OP) = ON cos a + NP sen a ==>>

==>> OA cos c = OA cos b cos a + NP sen a

Esta última linha resulta da expressão para ON usando o triângulo ONA, dada anteriormente. Precisamos agora encontrar uma expressão para NP. Usando o triângulo APN, temos:

NP = AN cos N = AN cos C = OA sen b cos C

A expressão acima faz uso do fato que o ângulo do triângulo APN com vértice em N é também o ângulo entre os planos OAC e OBC, sendo assim igual ao ângulo C do triângulo esférico. Já a substituição de AN = OA sen b vem do triângulo ONA.

Substituindo na expressão anterior temos então: