
Antes de mais nada, observemos um teorema chamado de Teorema da Reconstrução.
O teorema é desenvolvido como segue:
Considerem um campo vetorial genérico A(r) que
tende a zero no infinito. É verdade que

o que resulta das identidades vetoriais básicas; notem que os
operadores diferenciais agem sobre as variáveis sem linha. O Laplaciano
é proporcional a função delta, de onde segue,

Os operadores diferenciais próximos às integrais podem
ser deslocados para dentro destas e operados sobre as funções
1/|r-r'|. A seguir, as derivadas em r podem ser convertidas
no negativo das derivadas em r'. Como passo final, os operadores
assim gerados, via integração por partes ou via aplicações
do teorema da divergência, são conduzidos a atuarem sobre
os campos A(r'), ficando a expressão (41) com a forma
final

Esta é a expressão do Teorema da Reconstrução: um campo é determinado por duas fontes - seu divergente e seu rotacional.
No caso da eletrostática, e considerando A como o campo elétrico, por definição o rotacional é nulo. Conclusão: devemos conhecer o divergente para a (re)construção do campo. Mas vimos em tópicos passados que a componente predominante do campo é aquela cuja fonte pode ser promediada em pequenos volumes do espaço; a flutuação em torno da média é pequena. Portanto, o que realmente necessitamos saber para o cálculo do campo elétrico não é exatamente o valor exato de seu divergente, mas sim a quantidade

onde a barra indica uma média volumétrica definida genéricamente
da seguinte forma:

onde f é normalizada E localizada em uma região volumétrica
pequena que envolva um grande mas finito número de moléculas
do nosso sistema material:
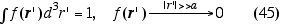
onde a denota a dimensão linear que caracteriza o tamanho do
pequeno volume onde as médias devem ser realizadas. Uma escolha
sugestiva, mas como veremos também ineficiente, para f seria f=1/DV,
DV= 4/3 p a3
dentro de uma região volumétrica de raio a,
com DV designando o volume da média.
Nestas condições teríamos de (44)

o que é simplesmente a média de G em torno do ponto r. Em geral devemos usar funções f que dependam suavemente de r para que possamos definir derivadas, como há de ficar claro a seguir. Em todo o caso, em termos de ordem de magnitude, usaremos f ~ 1/DV na região promediada, e f~0 fora dela. O ponto inicial é perceber que em (43), a média do divergente é o divergente da média. Com isto, uma vez que possamos avaliar o lado direito da expressão, teremos a fonte que entra em (42). Microscópicamente,

onde o somatório se estende sobre todas as partículas, j, carregadas de cargas qj, do sistema. De (43) necessitamos da quantidade promediada

As integrais podem ser avaliadas e ficamos com
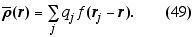
O somatório deve ser realizado sobre cada carga de cada molécula presente na região de interesse onde f é substancialmente diferente de zero. Denotemos a soma sobre moléculas e cargas na seguinte forma alternativa
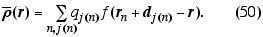
n é índice de molécula e j(n) designa a
carga j da molécula n. A posição da partícula
j foi representada como uma composição de sua posição
relativa dj(n) em relação ao centro de
massa rn da molécula da qual faz parte: rj=rn+dj(n).
dj(n)
é um número pequeno: em um grupo grande de moléculas
que compõe o volume DV, mede essencialmente a dimensão de
um destes "milhares" de moléculas.

Podemos, portanto, aplicar expansões de Taylor e escrever aproximadamente

Executando os somatórios primeiramente sobre as partículas de cada molécula e após sobre as moléculas, o primeiro membro do lado direito de (51) fornece a carga líquida do sistema divida pelo volume total, já que em ordem de magnitude, f é equivalente a 1/DV por força da condição de normalização - denotemos esta contribuição como rliquida (=qtotal/DV). O segundo membro pode ser escrito na forma


pn denota o momento de dipolo de cada molécula e P denota a densidade total dipolar, ou vetor de polarização - notem que mais uma vez usamos f~1/DV na região de interesse f->0 fora desta região.
Substituindo tudo em (43) ficamos com a seguinte expressão:

que é a expressão definindo o vetor deslocamente elétrico
D=e0E+P.