Nosso propósito passa a ser construir funções de Green para solucionar problemas de eletrostática. A função de Green satisfaz uma equação de Laplace com fonte puntual representada por uma função delta, com condições de contorno homogêneas: G(contorno)=0.

Tratemos de explorar uma maneira simples de calcular este tipo de configuração:

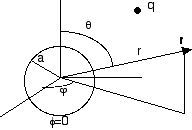
A figura a seguir demonstra, em coordenadas polar-esféricas, o que se tem em mente. Desejamos calcular o potencial total produzido por uma distribuição de cargas representada genéricamente por q, em um ponto arbitrário r, supondo que o potencial se anule na esfera de raio a.
 

Aqui convém separar o potencial total em r na parte "incidente", V_in , que depende somente das cargas q, sem nenhuma menção as condições de contorno, mais uma parte "espalhada", V_esp , que não possua fontes da região de interesse r>a, mas que deve ser escolhida de tal forma que o potencial total f=V_in+V_esp satisfaça a condição de contorno homogênea. Cabe notar que, para todos os efeitos, as fontes da parcela "espalhada" são cargas de superfície induzidas por q, que se formam na casca esférica. Em coordenadas polares, a partir da forma funcional do potencial incidente V_inc=V_inc(r,q,j) , o que se propõe como o potencial espalhado é o seguinte:
 

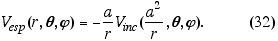
Este potencial certamente satisfaz f=0 no contorno r=a - verifique. O que nos resta saber é se o potencial satisfaz a equação de Laplace em r>a; este último ponto é essencial, pois a parte correspondente às fontes em r>a já está representada pelo potencial incidente nesta região. Em esféricas,
 

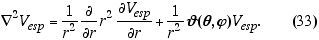
O operador J depende somente das coordenadas angulares e não será "tocado", já que a transformação de inversão se opera somente sobre a coordenada radial r. Usando (32) em (33), e definindo u=a²/r, temos:
 

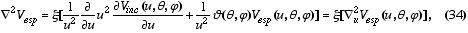
(x=u⁴/a⁴), o que nos indica que o Laplaciano de V_esp se cancela quando o Laplaciano de V_inc se cancelar. Ora, isto acontece para u<a, pois lá NÃO há fontes para o V_inc. Mas u<a significa r>a, que é precisamente a região dentro da qual estamos tentando construir o V_esp. Ou seja, com a forma (32) construimos uma função que satisfaz a equação de Laplace e que garante que a condição de contorno para f seja satisfeita - isto é, resolvemos nosso problema.

Problema: Façam o mesmo cálculo para problemas com coordenadas cilíndricas. Provem que V_esp=-a/r V_inc(a²/r,j,z) satisfaz a equação de Laplace para r>a, se V_inc a satisfizer para r<a. Mostre que V_esp+V_inc=0 sobre uma casca cilíndrica de raio a cujo eixo de simetria coincide com o eixo z.

Problema: Façam o mesmo para um plano coincidente com o plano xz. Específicamente, mostrem que V_esp=-V_inc(x,-y,z) satisfaz Laplace em y>0 se V_inc(x,y,z) satisfizer Laplace em y<0. Mostre que V_esp+V_inc =0 em y=0.

Examinemos uma aplicação interessante. Suponham que em r>a, no caso esférico, tenhamos uma carga q localizada em r_q. O potencial incidente, portanto, é
 

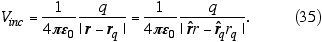
De (32) o potencial espalhado é calculado como
 

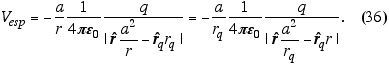
Notem que o versor radial não é tocado; tal versor só contém ângulos que não são alterados pelo teorema da inversão. Agora, como os versores tem módulo unitário,
 

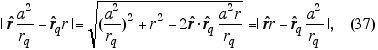
de onde finalmente ficamos com

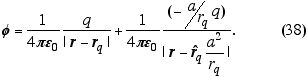
Isto permite concluir que o potencial espalhado pode ser encarado de maneira prática como produzido por uma carga -(a/r_q) q, colocada na posição , interior à esfera.