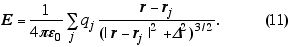
Como calcular o campo total devido a uma distribuição de cargas q_j localizadas nas posições r_j? Comecemos com o somatório formal:

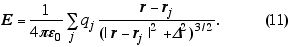
Quando o ponto de observação é distante de qualquer carga da distribuição com |r-r_j|>>D, e com |r-r_j|>>d onde d é a separação inter-cargas, um observador situado em r não distingue D e tampouco consegue separar partículas de suas vizinhas imediatas. Para este caso é razoável aproximar (11) pela integral de campo elétrico

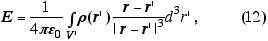
onde r designa a densidade (média) de partículas no meio e onde V’ indica o volume ocupado pelas cargas geradoras do campo; esta é a expressão convencional para o campo de uma distribuição.

O problema fica um pouco mais complexo quando o ponto de obsrvação está no interior da distribuição. Neste caso r e rj podem ficar próximos e as integrais devem ser regularizadas. Além disto devemos tratar de forma mais refinada a conversão do somatório para integral, já que a condição r-rj>> d não mais se cumpre para qualquer rj. Vamos então considerar um ponto arbitrário r e dividir o somatório (11) entre uma parcela que envolve cargas longínqüas a r, e cargas próximas a r. A parcela longínqüa continua com o mesmo formato de (12), enquanto a parcela próxima não pode mais ser substituida pela integração sobre uma densidade média. No entando, uma mera avaliação da ordem de magnitude das duas parcelas nos revela que a parcela longínqua escala como
rLL³/L³ ~rL, enquanto a parcela próxima escala como rll³/l³~rl. Como L>>l, a parcela próxima, que depende de l e de D, não contribui significativamente para o cálculo do campo e podemos considerar o limite da expressão para o campo quando l ->0. Desta forma (12) ainda é a expressão acurada para o campo mesmo quando o ponto de observação reside no interior da distribuição. A figura a seguir ilustra os procedimentos e aproximações.
 
 

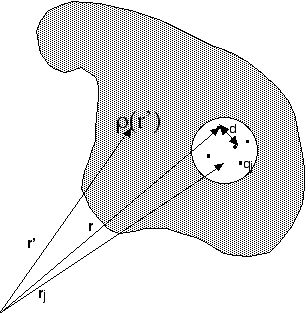
O tamanho da bola branca é dado típicamente por l e o tamanho da região hachurada é típicamente dado por L; isto faltou na figura.

A propósito, se as integrais em (12) se convertem em integrais bi ou unidimensionais (distribuições superficiais ou unidimensionais de carga) o campo final passa a depender de D. Calculem o campo na ponta de uma barra de comprimento L, na ponta da barra, use a regularização, e mostre que a integral depende de D. Isto é sinal de que a microscopia do problema fica importante aqui.

Agora tratemos de investigar a possibilidade de escrever o campo elétrico a partir de uma função escalar. Isto é relativamente simples se relembrarmos que

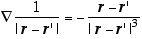expressão já deduzida anteriormente. Notem que como a contribuição que contem o fator D é também aquela não significativa para o cálculo do campo elétrico, por uma questão de economia não estamos escrevendo D nos denominadores.

De qualquer forma, com o uso da expressão acima, nosso campo adquire a forma:

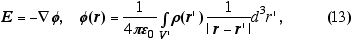
onde f é o assim denominado potencial eletrostático. Aplicando a divergência sobre o campo elétrico ficamos com a seguinte expressão

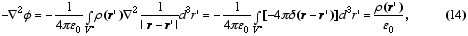
onde usamos da representação para a função delta em termos do Laplaciano do inverso da diferença de coordenadas.

Reunindo nossas informações, para o cálculo do potencial temos que satisfazer

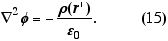
Se dividirmos nosso espaço em uma região interna a uma certa superfície e uma região externa a esta superfície de contorno, teríamos que resolver (15) na região interna, sujeita a f=f(C) sobre a superfície do contorno. A condição f=f(C) pode ser obtida diretamente de (13) com r=r_|contorno.

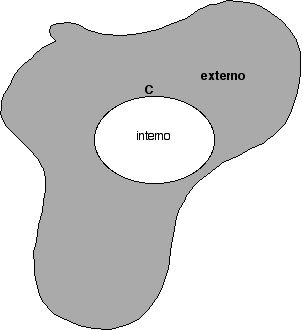
Observando a figura acima, o que fizemos foi substituir o efeito das cargas externas pelo valor do potencial no contorno. Será isto suficiente para uma solução unívoca do problema? Quem responde é o teorema da divergência aplicado a funções do tipo gradiente. Imaginem que ainda não saibamos que uma solução definida pela distribuição de cargas internas e pela condição de contorno seja única. Imaginemos que ao menos duas soluções satisfaçam

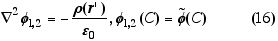
onde r é a densidade de cargas na região interna e f(C) o valor de f no contorno. Agora calculemos o comportamento de f₁-f₂; isto nos dá

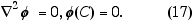
Agora calculemos via lei de Gauss

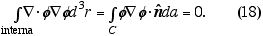
A primeira parcela pode ser desenvolvida como

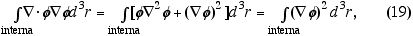
que é nula por força de (18). Ou seja, provamos que o gradiente do campo diferença é nulo. Como o campo diferença se cancela em C e com ele não varia a partir daí, deve ser nulo em todo o espaço interno.