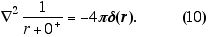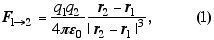
A expressão assintótica da força executada por uma partícula-fonte situada em uma posição genérica r₁ sobre uma partícula-teste situada em outra posição genérica r₂ é dada pela lei de Coulomb:

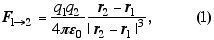
onde q_j são as cargas das partículas e e₀ a permissividade do meio que define a constante de proporcionalidade.

À grandeza F/q₂ dá-se a designação de campo elétrico. O campo elétrico em um posição assintótica r, gerado por uma carga q situada na origem é dado pela expressão discutida em aula, prontamente obtida de (1):

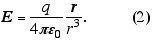
Quando se fala em "posição assintótica", subentende-se distâncias grandes se comparadas com as dimensões da partícula-fonte. Se por outro lado tomarmos r->0, claramente (1) indica problemas de singularidade com a teoria, ja que então o campo elétrico tenderia ao infinito. Como resolver tais problemas? Uma opção, adequada matematicamente e razoável físicamente, seria substituir o campo (2) por uma expressão refinada e regularizada:

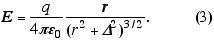
Desta forma o campo permanece finito em r=0. O que nos resta a fazer aqui é determinar que papel físico desempenha o fator D. Para tanto, usemos o teorme da divergência de Gauss, aplicado ao campo elétrico:

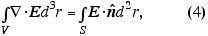
onde S é uma superfície, tomada como esférica, encapsulando o volume V em cujo centro se encontra a partícula-fonte. A normal ao lado direito de (4) é simplesmente dada por r/r e com o auxílio de (3) aplicada na região assintótica r>>D obtemos de (4):

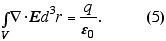
Isto nos leva a concluir que a divergência do campo elétrico, ao ser multiplicada pela permissividade, mede a densidade de carga da partícula teste, r=e₀ div E, onde r denota a densidade de cargas.

A divergência do campo elétrico, dado por (3), pode ser calculada com o auxílio da fórmula:

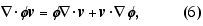
onde f é escalar e v, vetor. Aplicada em (3) obtemos:

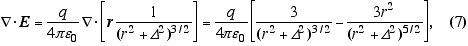
onde usamos

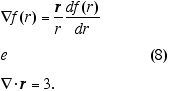
(Provem estas duas relações úteis) Um pouco de álgebra aplicada à (7) finalmente nos mostra que:

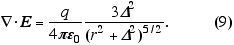
Como último tópico, tracemos o gráfico da divergência do campo elétrico, como abaixo:
 
 

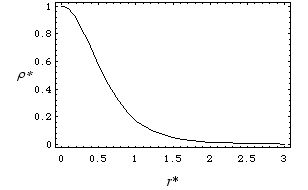
onde as seguintes quantidades normalizadas foram introduzidas:

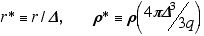O que se nota é um decaimento significativo da função r* na região r*~1, o que nos leva a interpretar D como a dimensão típica da fonte.

Com o campo das partículas assim regularizado, nossa próxima tarefa é o cálculo de campos de distribuições de partículas. Com a regularização, o campo deve ficar finito mesmo se o ponto
de observação coincide com a região onde as fontes estão presentes, o que apresentaria problemas de divergência caso a regularização não estivesse incorporada ao formalismo.

Como tarefa, (i) provem que a integral volumétrica da divergência do campo elétrico, eq. (9), fornece a carga q. Provem também que a divergência do campo se converte em uma função delta de Dirac quando D -> 0. Com isto encontrem e entendam a representação operacional