FIS01219 - Introdução a sistemas dinâmicos
Disciplina do Curso de
Graduação em Física
Carga: 4h
Semestre: 2012/2
Pré-requisitos: FIS01203 e FIS01205
Súmula
Sistemas autônomos de 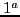 e
e 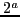 ordens; transformações
lineares do plano; preservação da área; aplicações uni e
multidimensionais; bifurcações, ciclos limites e caos; fractais,
atratores estranhos; conjuntos não-atratores estranhos; sincronização;
controle; formação de padrões; séries temporais.
ordens; transformações
lineares do plano; preservação da área; aplicações uni e
multidimensionais; bifurcações, ciclos limites e caos; fractais,
atratores estranhos; conjuntos não-atratores estranhos; sincronização;
controle; formação de padrões; séries temporais.
Objetivos
Familiarizar o aluno com os fundamentos de sistemas dinâmicos, com
as ferramentas de análise de sistemas dinâmicos e com a linguagem
utilizada na área.
Programa:
- Classificação dos sistemas dinâmicos
- Sistemas a tempo contínuo, sistemas autônomos e não-autônomos,
sistemas conservativos, dissipativos, noções de
estabilidade. Solução geral para sistemas lineares.
- Sistemas não-lineares de tempo contínuo. Equivalência
Topológica. Teoremas locais para sistemas não-lineares. Teoria da
variedade central, formas normais.
- Oscilações lineares e não-lineares. Ciclo limite.
- Bifurcações em sistemas de tempo contínuo. Estabilidade
estrutural. Bifurcações em codimensão um. Bifurcações homoclínica e
heteroclínica.
- Caracterização da dinâmica caótica. Atratores, expoente de
Lyapunov, esticamentos e dobras, entropia de Shanon, dimensões de um
atrator.
- Sincronização. Sincronização de oscilador por força externa.
Sincronização de dois ou mais osciladores. Sincronização de sistemas
caóticos.
Método de Trabalho
Aulas expositivas, experiências numéricas em laboratório computacional.
Avaliação
- 2 avaliações e um seminário (conforme tópicos abaixo).
(conforme tópicos abaixo).
* -
Presença e participação nos seminários (dos colegas) conta 3 pontos na nota
do seminário.
Tópicos para Seminário
- Sistemas não-lineares a tempo discreto e mapa logístico ;
- Pêndulo simples e sistemas equivalentes ;
- Seção de Poincaré e mapa de Poincaré ;
- Entropia de Shanon ;
- Dimensões de um atrator ;
- Reconstrução de Takens ;
- Modelo de Lotka-Volterra ;
- Modelo SIR ;
- Osciladores de fase acoplados: quasiperiodicidade e
travamento ;
- Sincronização ;
- Mapa circular, escada do diabo e línguas de Arnold ;
- Modelos de neurônios ;
- Reações químicas: Michaelis-Menten, Belousov-Zhabotinsky e o
``brusselator'' ;
- Controle de caos ;
Bibliografia
- Sistemas Dinâmicos, Luiz Henrique Alves, Ed. Livraria da
Física, 2002.
- Dissipative Structures and weak turbulence, Paul
Manneville, Academic Press, 1990.
- Synchronization, A. Pikovsky, M. Rosenblum e Jürgen
Kurths, Cambridge Nonlinear Science Series 12, 2003.
- Elements of Differentiable Dynamics and Bifurcation Theory, David
Ruelle, 1989. Academic Press. ISBN 0-12-601710-7
- Chaos. An introduction to dynamical systems, Kathleen
T. Alligood, Tim D. Sauer and James A. Yorke, Springer
Verlag, 2000. ISBN 0-387-94677-2
- Nonlinear Dynamics and Chaos: With Applications to Physics,
Biology, Chemistry and Engineering, Steven H Strogatz, Addison
Wesley, 1994. ISBN 0-201-54344-3
- Differential Equations, Dynamical Systems, and an
Introduction to Chaos, Morris W. Hirsch, Stephen Smale,
Academic Press, 2003. ISBN 0-12-349703-5
Leonardo Gregory Brunnet
2012-08-26
![]() e
e ![]() ordens; transformações
lineares do plano; preservação da área; aplicações uni e
multidimensionais; bifurcações, ciclos limites e caos; fractais,
atratores estranhos; conjuntos não-atratores estranhos; sincronização;
controle; formação de padrões; séries temporais.
ordens; transformações
lineares do plano; preservação da área; aplicações uni e
multidimensionais; bifurcações, ciclos limites e caos; fractais,
atratores estranhos; conjuntos não-atratores estranhos; sincronização;
controle; formação de padrões; séries temporais.
![]() (conforme tópicos abaixo).
(conforme tópicos abaixo).