Radiação e matéria

Radiação térmica - Teoria de Planck

Podemos constatar a existência da radiação térmica ao aproximarmo-nos de uma brasa incandescente. Mesmo se o ar ao nosso redor estiver frio, percebemos um aquecimento da nossa pele. Nesta situação, a maior parte do calor que nos atinge não se propaga por convecção no ar, e sim na forma de radiação eletromagnética.

Também percebemos esta radiação na cor avermelhada adquirida pelo carvão ao queimar. O carvão é normalmente preto, ou seja não reflete a luz, mas ao alcançar uma temperatura suficientemente alta, passa a emitir na parte visível do espectro uma quantidade de radiação suficiente para observação.

Se observarmos o aquecimento de um pedaço de ferro com uma fonte intensa de calor, por exemplo uma forja, poderemos notar, além do rápido aumento com a temperatura da quantidade de radiação emitida, uma modificação na cor do objeto: após tornar-se vermelho, o objeto passará a adquirir uma cor branca ou até azulada. Isto indica que a distribuição da radiação em comprimento de onda desloca-se com o aumento da temperatura para valores menores. Equivalentemente, a distribuição da radiação em freqüência desloca-se para valores maiores.

O fato de existir uma correlação entre temperatura e emissão de radiação não é em si surpreendente. Afinal, de acordo com a visão corpuscular da matéria, temperatura é uma medida da agitação randômica das partículas. Como as partículas que constituem a matéria possuem cargas e cargas em movimento acelerado emitem radiação, o fenômeno de radiação térmica é qualitativamente entendível na luz da teoria clássica. Porém, como veremos, esta teoria revela-se incapaz de fornecer uma descrição quantitativa aceitável.

Radiância espectral

A quantidade adequada para caracterizar quantitativamente a emissão de radiação por um corpo em equilíbrio térmico à temperatura T é a radiância espectral R(n), definida tal que R(n) dn fornece a quantidade de energia emitida pelo corpo, por unidade de tempo e de área, no intervalo de freqüência [n, n + dn].

A radiância espectral depende do material considerado. É uma função contínua na qual estão presentes picos e vales que são característicos do material. A radiação térmica corresponde à parte contínua.

Um resultado importante é que a distribuição espectral de absorção é igual à distribuição de emissão. Já encontramos uma afirmação semelhante no caso dos espectros de linhas. No que diz respeito à radiação térmica, significa que um bom emissor será também um bom absorvedor. Para entender o porque desta lei, basta imaginar um sistema de dois corpos em equilíbrio térmico, sendo um deles um emissor mais eficiente que o outro. Obviamente, o sistema poderá permanecer em equilíbrio somente se o corpo que emitir mais também absorver mais radiação. Outro argumento é que o processo de aborção é o inverso do processo de emissão, e ambos são favorecidos pela maior mobilidade das cargas no material, como ocorre no caso de uma antena.

[1] Max Karl Ernst Planck, físico alemão, 1858-1947.

Corpo negro

Um corpo cuja superfície é preta e fosca, um quadro negro por exemplo, aproxima-se bastante de um corpo negro. Porém, um corpo negro a temperatura alta pode ser bastante brilhante e colorido. Astrônomos frequentemente aproximam uma estrela por um corpo negro.

Cavidade

Outro exemplo de sistema que aproxima bastante o corpo negro é uma cavidade, um recinto fechado feito de um material que não deixa passar a radiação e no qual há um pequeno furo. Mesmo se a parede interna da cavidade absorve apenas parte da radiação que incide sobre ela e reflete o resto, o grande número de reflexões - veja a figura - resulta numa absorção praticamente completa.

Cavidade

É fácil demonstrar que existe uma relação simples entre a radiância espectral e a densidade espectral de energia r(n) na cavidade, definida tal que r(n) dn seja a energia por unidade de volume, associada à radiação cuja freqüência esteja no intervalo [n, n + dn]. A relação é simplesmente

(5-1)

onde c é a velocidade da luz. Veja os detalhes.

Fenomenologia

A radiância espectral do corpo negro apresenta as seguintes características (veja a figura):

• tende para zero, tanto para freqüências muito grandes quanto para freqüências muito pequenas;.
• possui um máximo para uma certa freqüência, cujo valor aumenta com a temperatura;
• para qualquer freqüência dada, a radiância espectral aumenta rapidamente com a temperatura.

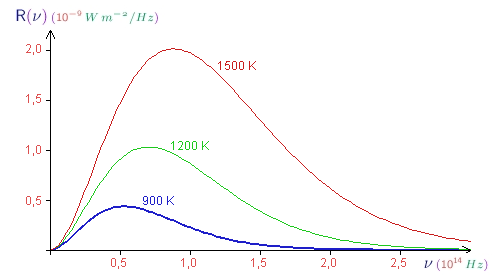Radiância espectral do corpo negro

As duas últimas propriedades citadas são descritas mais quantitativamente por leis fenomenológicas.

• A lei de Wien², afirma que a freqüência n_max para a qual a radiância espectral alcança o seu valor máximo aumenta proporcionalmente à temperatura:

  (5-2)

  O valor experimental da constante de proporcionalidade é

  (5-3)

• A lei de Sefan³-Boltzmann⁴ estipula que a potência total emitida por unidade de área - ou seja, a integral da radiância espectral sobre todas as freqüências, é proporcional à quarta potência da temperatura:

  (5-4)

  A constante s, conhecida como constante de Sefan, vale

  (5-5)

[2] Wilhelm Wien, físico alemão, 1864-1928.
[3] Josef Stefan, físico austriaco, 1835-1893.
[4] Ludwig Boltmann, físico austriaco, 1844-1906.

Teoria clássica

• a matéria é composta de partículas carregadas;
• temperatura é agitação randômica das partículas;
• cargas em movimento acelerado emitem radiação eletromagnética.

• a energia média E(n) de uma onda eletromagnética de freqüência de freqüência n;
• o número n(n) dn de ondas por unidade de volume, cuja freqüência esteja no intervalo [n, n + dn].

(5-6)

(5-7)

Energia média de uma onda

O resultado previsto pela teoria clássica para a energia média de uma onda pode ser justificado invocando-se o teorema de equipartição da energia, que já encontremos na nossa breve discussão da teoria cinética dos gáses, e que nós diz que, num sistema em equilíbrio térmico a temperatura T, a energia cinética média por grau de liberdade vale

(5-8)

Uma onda eletromagnética num dado estado de polarização linear é análoga a um oscilador harmônico unidimensional, cujo exemplo canônico é o sistema massa-mola. Para este sistema, sabemos que a energia potencial média (sobre um período) é igual à energia cinética média:

(5-9)

Portanto, a energia total média é

(5-10)

Este resultado deve valer então também para a onda eletromagnética. Vale notar que a energia média é independente da freqüência.

Contagem das ondas

O cálculo do número de ondas num intervalo de freqüência será facilitado se considerarmos uma cavidade cujas paredes sejam perfeitamente condutoras. Isto é lícito, pois, como já mencionado, uma cavidade comporta-se como um corpo negro, independentemente da natureza das suas paredes. Sendo a parede condutora, poderemos impor condições de contorno simples sobre o campo eletromagnético: a componente do campo elétrico paralela à parede deverá anular-se pois, caso contrário, haveria um deslocamento de cargas na parede até que a condição em questão seja realizada.

No intuito de expor o procedimento de contagem das ondas com maior simplicidade, vamos considerar primeiro um modelo "brinquedo": uma cavidade unidimensional de comprimento L. Neste caso, o campo elétrico é descrito por uma onda estacionária da forma

(5-11)

onde introduzimos o número de onda k e a freqüência angular w. Lembramos que estas quantidades estão relacionadas com o comprimento de onda l e a freqüência n por

e

(5-12)

Lembramos também que, já que a velocidade de fase de uma onda eletromagnética é c, temos

(5-13)

Para que o campo elétrico se anule sobre as "paredes" (as extremidades da caixa unidimensional), o número de onda deve satisfazer a condição

(5-14)

com q = 1, 2, 3... De (5-12) e (5-13), seguem os valores possíveis da freqüência:

(5-15)

O número de número N(n) Dn de ondas no intervalo de freqüência Dn será dado pelo número Dq de valores de q correspondentes:

(5-16)

Contagem das ondas numa caixa unidimensional e numa caixa cúbica

Para passar ao caso realista de uma cavidade cúbica, basta considerar o número de onda como um vetor e exigir que o campo elétrico seja nulo sobre cada par de paredes, paralelas a cada um dos três eixos de coordenadas. Isto nós leva a três equações análogas a (5-14):

(5-17)

onde q_x, q_y e q_z são números inteiros positivos. O número de ondas no intervalo de freqüência Dq será dado pelo número de valores destes inteiros que correspondem a pontos num oitavo de casca esférica de raio q e espessura Dq. Como os pontos formam uma rede cúbica de intervalo unitário, o número de pontos é igual ao volume, ou seja:

(5-18)

com

(5-19)

Utilizando de novo a relação (5-14), obtemos

(5-20)

O número de ondas por unidade de volume no intervalo de freqüência [n, n + dn] será obtido no limite de um intervalo infinitesimal, dividindo-se a expressão acima pelo volume L³ da caixa e multiplicando-se por dois, pois devemos lembrar que uma onda eletromagnética propagando-se numa dada direção com uma dada freqüência pode estar em dois estados distintos de polarização. O resultado final desta contagem é portanto

(5-21)

Catástrofe do ultravioleta

Já que, seguindo a teoria clássica, a energia média de uma onda eletromagnática à temperatura T é simplesmente dada por kT, a densidade de energia de cavidade para freqüências em [n, n + dn] é

(5-22)

e, por (5-1), a radiância espectral é

(5-23)

Este resultado fornece uma descrição aceitável apenas para pequenos valores da freqüência [veja a figura]. À medida que a freqüência cresce, ele diverge cada vez mais dos dados experimentais. Pior ainda, ele é físicamente inaceitável pois ele implicaria que a potência total emitida, por unidade de área, pelo corpo negro - a integral da radiância sobre todas as freqüências - seria infinita. Assim, a teoria clássica revela-se não apenas incapaz de reproduzir a fenomenologia, mas intrínsecamente paradoxal. Esta situação é frequentemente qualificada de catástrofe do ultravioleta, em referência à parte de alta freqüência do espectro, na qual o problema se manifesta.

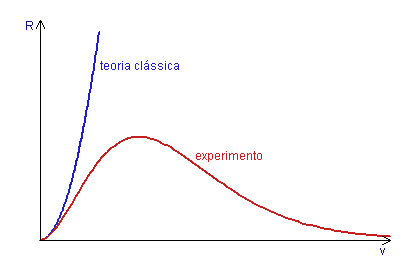Radiância espectral do corpo negro: fracasso da teoria clássica

[5] Lord Rayleigh (John William Strutt), físico inglês, 1843-1919.
[6] James Jeans, astrofísico inglês, 1877-1946.

Teoria de Planck

• já que a teoria clássica descreve adequadamente o limite de baixa freqüência do espectro, o resultado clássico deve ser válido neste limite:

  (5-24)

• já que o número de ondas cresce com a freqüência mas a radiância espectral tende a zero, é necessário que a energia média também tenda a zero - suficientemente rapidamente - neste limite:

  (5-25)

(5-26)

Na física clássica, a energia é uma variável contínua e deve-se na verdade interpretar p_C(E) dE como a probablidade de obter um valor da energia no intervalo [E, E + dE]. O subscrito C serve para lembrar que trata-se do caso clássico. A constante A_C correspondente é determinada pela condição

(5-27)

que leva a

(5-28)

Podemos verificar que o cálculo da energia média a partir desta distribuição de probabilidade leva ao resultado já discutido:

(5-29)

onde realizemos uma integração por parte e usemos o resultado anterior.

Assim, se a energia for uma variável contínua, não há como escapar do resultado clássico. Planck percebeu que o mesmo cálculo poderia levar ao comportamento desejado se a energia fosse quantizada em múltiplos inteiros de um quantum que seja uma função adequada da freqüência:

(5-30)

com n = 1, 2, 3 ... e DE uma função de n.

Cálculo da energia média de uma onda

Para entender o porque desta intuição, basta notar que o cálculo da energia média envolve basicamente a integral da função E p(E), plotada no gráfico acima. É fácil verificar que esta função possui um máximo para E = kT e torna-se muito pequena para E >> kT. Pela interpretação da integral como área contida entre a curva que representa a função e o eixo das abscissas, podemos ver que se DE << kT, o cálculo "quantizado" da energia média fornecerá um valor praticamente igual ao resultado clássico. Em contrapartida, se DE >> kT, o cálculo quantizado fornecerá um valor muito pequeno para a energia média, pois não haverá contribuição da região na qual a distribuição de Boltzmann prevê uma probabilidade significativa. Concluimos que podemos conseguir o comportamento desejado (5-24)-(5-25) de E(n) se DE for muito pequeno para pequenos valores de n e tornar-se grande para valores muito grandes de n. Ou seja, se o quantum de energia for uma função crescente da freqüência.

Planck experimentou a mais simples função com estas caraterísticas:

(5-31)

com h uma constante. Apesar de ter sido descrita pelo próprio Planck como uma "tentativa desesperada", esta hipótese não apenas revelou-se adequada para a descrição da radiação de corpo negro, mas constitui-se no ponto de partida de uma nova física.

Detalharemos agora o cálculo da energia média de uma onda baseado na hipótese de Planck. Quando a energia toma valores discretos, a integral calculada acima é substituída por uma soma sobre os possíveis valores poderados pelas respectivas probabilidades:

(5-32)

onde o denominador garante que a soma das probabilidades é igual à unidade. Usando (5-30) e (5-31), temos

(5-32)

onde introduzimos, por conveniência, a variável adimensional

(5-33)

e definimos a função

(5-34)

É facil ver que podemos re-escrever esta função na forma

(5-35)

O estudo das séries geométricas fornece o resultado

para

(5-36)

Para X = e^-a, isto nós fornece o valor da série presente na equação (5-35):

(5-37)

Obtemos portanto

(5-38)

Inserindo isto na equação (5-32), com a dada por (5-33), obtemos a expressão final fornecida pela teoria de Planck para a energia média de uma onda eletromagnética de freqüência n numa cavidade à temperatura T:

(5-39)

Podemos facilmente verificar que esta função possui as propriedades desejadas, pois para grandes valores de n podemos desprezar o segundo termo no denominador e obter

(5-40)

que satisfaz (5-25) já que a exponencial vence qualquer potência. Para pequenos valores de n, podemos expandir a exponencial em e ficar com os dois primeiros termos apenas:

(5-41)

Re-obtemos o resultado clássico neste limite, como desejado [veja (5-24)].

Em posse da expressão da energia média (5-39), podemos calcular a densidade espectral de energia de cavidade usando (5-6) com (5-21). Obtemos:

(5-42)

A radiância espectral é dada semelhantemente por (5-7):

(5-43)

Planck determinou a constante h de maneira a obter a melhor descrição possível da radiância espectral do corpo negro. Nos anos subsequentes, tornou-se claro que tratava-se de uma nova constante fundamental que ia permear toda a física. O próprio Planck denominou-a quantum de ação, por ela ter a mesma unidade que a ação introduzida na formulação Lagrangiana da mecânica clássica, qual seja: energia x tempo. O valor atualmente aceito da constante de Planck é

(5-44)

Não é difícil conferir que a teoria de Planck explica as leis fenomenológicas discutidas anteriormente. A potência total emitida pelo corpo negro, por unidade de área, é dada pela integral da radiância espectral sobre todas as freqüências:

(5-45)

onde fizemos uma troca de variável de n para a, já introduzida em (5-33). Consultando uma tabela de integrais, descobrimos que

(5-46)

Assim, a teoria de Planck leva à lei de Stefan-Boltzmann (5-4) e fornece a expressão da constante de Stefan em termos das constantes fundamentais h, k e c:

(5-47)

A freqüência n_max para a qual a radiância espectral alcança um máximo é obtida impondo que a derivada desta função se anule. Escrita em termos da variável a, a condição é

(5-48)

cuja solução é

(5-49)

Usando (5-33), obtem-se

(5-50)

que está em acordo com a lei de Wien (5-2) e permite calcular a constante presente nesta lei fenomenológica a partir das constantes fundamentais h e k.