Os Dez Mais Belos Experimentos da Física
A edição de setembro/2002 da revista Physics World apresenta o resultado de uma enquete realizada entre seus leitores sobre o mais belo experimento da física. Nas páginas seguintes, os dez mais votados serão descritos nos contextos teóricos em que se inserem.
- Experimento da dupla fenda de Young, realizado com elétrons
- Experimento da queda de corpos realizada por Galileu
- Experimento da gota de óleo, realizada por Millikan
- Decomposição da luz solar com um prisma, realizada por Newton
- Experimento de interferência da luz, realizada por Young
- Experimento com a balança de torsão, realizada por Cavendish
- Medida da circunferência da terra, realizada por Eratóstenes
- Experimentos sobre o movimento de corpos num plano inclinado, realizados por Galileu
- Espalhamento de Rutherford
- O Pêndulo de Foucault
Experimento da dupla fenda de Young
O primeiro e o quinto experimentos representam diferentes circunstâncias de um mesmo tipo de experimento, isto é, do experimento da dupla fenda de Young. Sir Isaac Newton (1642-1727) defendia a hipótese de que a luz era constituída de corpúsculos. Os principais fenômenos óticos (reflexão e refração) podiam ser explicados com o uso da teoria corpuscular. Este modelo era combatido por Christiaan Huygens (1629-1695), que defendia a teoria ondulatória. No entanto, a autoridade científica de Newton fez prevalecer sua teoria por mais de um século. Por volta de 1801, uma bela experiência realizada por Thomas Young (1773-1829) resolveu a questão favoravelmente a Huygens. A experiência de Young provou que a luz era uma onda, porque os fenômenos da difração e da interferência, por ele descobertos, eram características exclusivamente ondulatórias. Veremos mais adiante, que a dualidade partícula-onda, proposta por de Broglie, sugeriu a possibilidade de ocorrência desses fenômenos para o caso de partículas.
| A minha forma preferida de visualizar o comportamento ondulatório é através de ondas geradas numa cuba de ondas, um dispositivo bastante usado nos laboratórios universitários e em alguns colégios. Ondas circulares são geradas quando a ponta de um bastão toca na água em iguais intervalos de tempo, conforme ilustra a figura ao lado. O detetor pode ser uma rolha de cortiça. A intensidade da onda, ou a energia transferida pela onda, é proporcional à altura alcançada pela rolha. A figura mostra um arranjo com duas fendas. Vejamos o que acontece se a fenda inferior for fechada. | 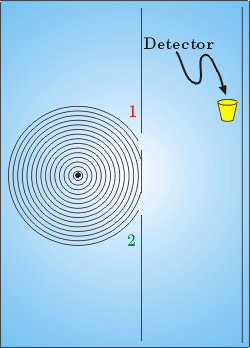
|
| A distribuição de energia que chega no anteparo é dada pela curva vermelha. O formato desta curva varia conforme a largura da fenda, e o comprimento de onda (separação entre os círculos da figura). Se a largura diminuir, a onda "se espalha" ao passar pela fenda. É como se uma nova onda circular fosse "criada" na fenda. | 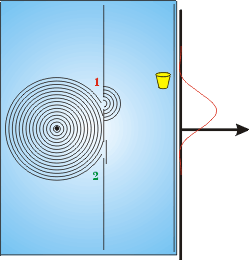
|
| Fechando a fenda superior e abrindo a inferior, a distribuição de energia mantém seu formato, mas desloca-se para a posição em frente à fenda inferior. Vejamos o que acontece quando as duas fendas permanecem abertas. | 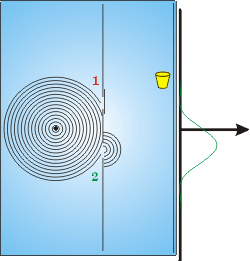
|
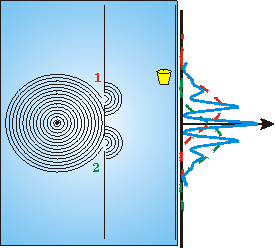
| As curvas tracejadas (verde e vermelha) representam os resultados anteriores, enquanto a curva contínua (azul)
representa o que se observa. Esta curva não apresenta uma relação simples com as anteriores. Por exemplo, não é
simplesmente a soma nem a subtração das curvas
anteriores. Diferentemente das curvas anteriores, esta curva obtida com as duas fendas abertas apresenta vários
pontos onde a intensidade é nula. Entre estes pontos, a intensidade apresenta valores diferentes. Este foi o surpreendente resultado obtido por Young, quando ele fez este tipo de experiência usando a luz. O fenômeno responsável pelo resultado é denominado interferência, e a curva é usualmente denominada padrão de interferência.
Vejamos o que aconteceria com uma experiência similar realizada com partículas. |
 |
| Podemos usar balas atiradas contra fendas feitas num anteparo impenetrável. Isto é, as balas só ultrapassam o anteparo através das fendas. O detetor pode ser uma lata com areia. O experimento é realizado assim: o detetor é colocado em determinada posição enquanto a espingarda fica disparando. Ao final de determinado intervalo de tempo, conta-se o número de balas coletadas pelo detetor. A distribuição de balas atingindo diferentes posições é obtida pela repetição desse procedimento, com o detetor sendo colocado nas diversas posições. | 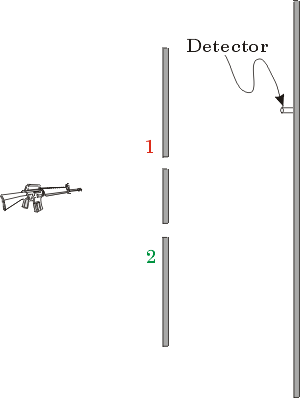 |
| Com a fenda inferior bloqueada, a distribuição de balas atingindo o anteparo tem o formato da figura ao lado, centralizada no ponto em frente à fenda superior. | 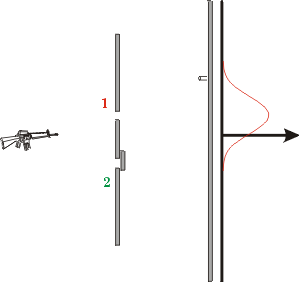 |
| Com a fenda superior bloqueada, a distribuição tem o mesmo formato da anterior, mas passa a ser centralizada no ponto em frente à fenda inferior. | 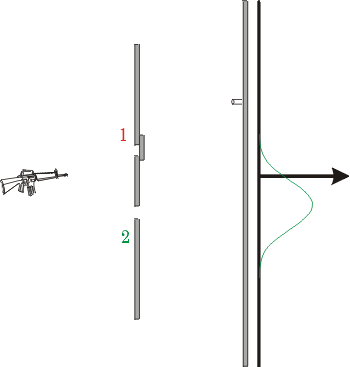 |
| Com ambas as fendas abertas, a distribuição é a soma das anteriores. Veja que este resultado é completamente diferente daqueles obtidos com ondas de água ou com luz. Isto é, as partículas não apresentam os fenômenos de difração e interferência. Portanto, como se trata de fenômeno exclusivamente ondulatório, Young concluiu que a luz é uma onda (conforme o modelo de Huygens) e não um conjunto de corpúsculos, conforme o modelo de Newton. | 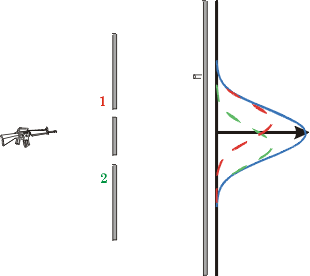 |
Em 1905, para explicar o efeito fotoelétrico Einstein usou uma idéia similar a de Newton, segundo a qual, ao invés de pensarmos na luz como uma onda, deveríamos imaginá-la constituída de corpúsculos, denominados fótons. Com o sucesso da explicação do efeito fotoelétrico, ficou provado que a luz tem um caráter dualístico. Dependendo das circunstâncias, poderia ser vista como onda (apresentando, p.ex. o fenômeno da interferência e da difração), ou como partícula (apresentando o efeito fotoelétrico).
Completando o ciclo da dualidade partícula-onda, Louis de Broglie sugeriu o contrário, isto é, que uma partícula poderia apresentar comportamento ondulatório. De modo análogo ao caso da luz, o caráter ondulatório de uma partícula deveria ser comprovada através de uma experiência de difração ou interferência. O trabalho de de Broglie foi publicado em 1923, e já em 1927, Davisson e Germer realizaram uma experiência na qual se observava a difração de um feixe de elétrons através de um cristal de níquel. Embora esta tenha sido a primeira experiência comprovando o caráter ondulatório de uma partícula, ela não é uma experiência do tipo dupla fenda como a que Young realizou com a luz. Este tipo de experiência só foi realizada com elétrons em 1961, por Claus Jönsson.
Créditos e agradecimentos
Agradecemos ao Dr. David M. Harrison, do Departamento de Física da Univ. de Toronto, a autorização para usar as ilustrações do seu excelente site The Feynman Double Slit.
Bibliografia
- BASSALO, J.M.F. Crônicas da Física. Belém: Gráfica e Editora Universitária (1987).
- BEISER, A. Modern Physics: an introductory survey. London: Addison-Wesley (1968).
- d’ABRO, A. The rise of the new physics. New York: Dover (1951).
- DE BROGLIE, L. La physique nouvelle et les quanta. Paris: Flamarion (1937), cap. VIII.
- FEYNMAN, R.P., LEIGHTON, R.B., SANDS, M. The Feynman lectures on physics. Addison-Wesley (1969).
- FUCHS, W.R. Física Moderna. São Paulo: Editora Polígono (1972).
- HALLIDAY, D., RESNICK, R. Fundamentos de Física, v. 4. Ótica e Física Moderna. Rio de Janeiro: Livros Técnicos e Científicos (1991).
- JÖNSSON, C. Electron diffraction at multiple slits. American Journal of Physics 42 (1974) 4-11.
- SEGRÈ, E. From X-Rays to Quarks. New York: W.H. Freeman and Company (1980).
- TIPLER, P.A. Física Moderna. Rio de Janeiro: Guanabara Dois (1981)
- TONOMURA, A., ENDO, J., MATSUDA, T., KAWASAKI, T. Demonstration of single-electron buildup of an interference pattern, American Journal of Physics 57 (1989) 117-120.
- ZELLINGER, A., GÄHLER, R. SHULL, C.G., TREIMER, W. MAMPE, W. Single- and double-slit diffraction of neutrons. Reviews of Modern Physics 60 (1988) 1067-1073.
Experimentos de Galileu
| O segundo experimento mais belo da física teria sido realizado por Galileu na torre de Pisa. Embora, de acordo com o historiador Alexandre Koyré, isso não passa de uma lenda, é interessante discutir o que pretendia Galileu com este tipo de experiência. O principal objetivo de Galileu era combater a hipótese de Aristóteles, segundo a qual a velocidade de queda de um corpo é proporcional a seu peso. Para Galileu, o peso não deveria ter qualquer influência na velocidade de queda. A comprovação seria simples: bastava jogar do alto da torre corpos com diferentes pesos e medir o tempo de queda. Há relatos na literatura de que bolas de 10 gramas e de 1 grama teriam sido lançadas, todas chegando ao solo ao mesmo tempo. Isso poderia ser facilmente observado se não houvesse a resistência do ar e outros fatores, como a forma e o material dos corpos lançados. Na verdade, a afirmação "todas chegando ao solo ao mesmo tempo" só seria rigorosamente verdadeira se a experiência fosse realizada no vácuo. |  |
| Galileu vislumbrou uma alternativa ao experimento da torre de Pisa para investigar a relação entre o peso de um corpo e sua velocidade de queda. Esta alternativa constitui o oitavo experimento mais votado. Os experimentos sobre o movimento de corpos num plano inclinado são detalhadamente descritos por Galileu na sua famosa obra Discursos sobre duas novas ciências. | 
|
Bibliografia
- BASSALO, J.M.F. Crônicas da Física. Belém: Gráfica e Editora Universitária (1987).
- GALILEU GALILEI Duas novas ciências. São Paulo: Nova Stella Editorial.
- HALLIDAY, D., RESNICK, R. Fundamentos de Física, v. 1. Mecânica. Rio de Janeiro: Livros Técnicos e Científicos (1991).
- KOYRÉ, A. Estudos de história do pensamento científico. Rio de Janeiro: Forense Universitária (1991).
- LUCIE, P. Física básica 1. A gênese do método científico. Rio de Janeiro: Editora Campus (1977).
- THUILLIER, P. De Arquimedes a Einstein. A face oculta da invenção científica. Rio de Janeiro: Jorge Zahar Editor (1994).
Experimento da gota de óleo, realizada por Millikan
Além do papel desempenhado no contexto do desenvolvimento científico do início do século, o experimento da gota de óleo de Millikan desempenha hoje papel importante no ensino da física moderna; trata-se de um dos clássicos experimentos freqüentemente realizados nos laboratórios de física moderna.
Físico experimental reconhecidamente habilidoso, Millikan exerceu forte influência no desenvolvimento da ciência norte-americana, não apenas pela realização de pesquisa relevante, como também pela competência administrativa, conforme brevemente discutido a seguir. Entre todos os seus trabalhos, aqueles referentes ao experimento da gota de óleo e à comprovação da equação de Einstein para o efeito fotoelétrico apresentam significados especiais porque simbolizam o Prêmio Nobel ganho em 1923.
Com relação ao experimento da gota de óleo, há uma controvérsia quanto ao nível de participação do seu estudante Harvey Fletcher, que, em manuscrito postumamente publicado, sugere que Millikan o "convenceu" de que o primeiro trabalho da série deveria levar apenas a assinatura do "Chefe". Para "infelicidade" de Fletcher, esse foi o "paper" que ficou famoso.
O texto a seguir é baseado em artigo publicado na Revista Brasileira de Ensino de Física (dos Santos, 1995), no qual é apresentada a versão de Fletcher, detalhando as etapas iniciais da construção do equipamento. Também é feita uma análise de como a questão é apresentada em outras fontes bibliográficas. A descrição de Fletcher reveste-se de importância porque, aparentemente, não há na literatura uma descrição tão detalhada dessa fase do trabalho de Millikan, nem mesmo apresentada pelo próprio.
Medida da carga do elétron: de Thomson a Millikan
Tendo como referências básicas o ensaio de Holton e o livro de Anderson, objetiva-se com esta seção apresentar uma breve descrição da evolução dos métodos baseados na câmara de bolhas, desde Thomson até Millikan.
Por volta de 1897, C.T.R. Wilson, um dos estudantes de Thomson, desenvolveu a sua famosa câmara de bolhas, ou câmara de nuvens, que permitiu o desenvolvimento de pesquisas revolucionárias na área da física moderna. O uso da câmara de Wilson para a determinação da carga do elétron fundamenta-se no fato de que íons gasosos servem como núcleos de condensação de vapor d’água. Em outras palavras, os íons são decorados por gotículas do vapor supersaturado. Os íons são produzidos com um feixe de raios X, ou com um feixe de raios gama emitidos por uma fonte radioativa.
Em 1851, Sir George Stokes mostrou que uma gota esférica, de raio a e densidade r, caindo sob a ação de um campo gravitacional g, num fluido uniforme de viscosidade h , atinge uma velocidade terminal uniforme dada por v = (2/9)(ga2r/h ). Sendo este movimento exatamente o mesmo daquele experimentado por cada gota ionizada na câmara de Wilson, Thomson usou a relação de Stokes para estimar o raio médio das gotículas. Não cabe aqui apresentar o trabalho de Thomson detalhadamente; ele é importante pela introdução da câmara de bolhas, e pelo uso da relação de Stokes, mas as dificuldades metodológicas imediatamente apontaram para a necessidade de aperfeiçoamentos. Para compreender essa necessidade e as motivações das tentativas seguintes, vejamos, mesmo que superficialmente, algumas etapas do método de Thomson. A carga total da nuvem de gotículas era medida com um eletrômetro, de modo que a carga de cada gotícula era obtida pela média; o número de gotículas era obtido através de um complicado processo de medidas e cálculos, começando pela medida da velocidade da nuvem e passando pelo uso da relação de Stokes. O melhor valor obtido por Thomson foi da ordem de 1.1x10-19 coulomb.
Em 1903, outro estudante de Thomson, H.A. Wilson, implementou duas novidades nesse método. A primeira foi a decisão de observar apenas a parte superior de cada nuvem, porque consistia de gotículas menores e que se deslocavam mais lentamente. A segunda e mais importante novidade, foi a introdução de um campo elétrico na mesma direção do campo gravitacional. O tratamento matemático desse método é apresentado no livro de Anderson, não cabendo aqui repeti-lo. Todavia, é interessante apresentar a expressão final para a carga do elétron, usada por Thomson e Wilson:
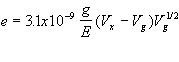
onde g é o módulo da aceleração gravitacional,
E é o módulo do campo elétrico aplicado, Vx
e Vg são, respectivamente, os módulos das velocidades
terminais com e sem campo elétrico. A carga do elétron obtida
com este método oscilava em torno de 1.04x10-19 coulomb.
Millikan e seu estudante Begeman iniciaram, em 1907, a repetição do experimento de H.A. Wilson. A seqüência de tentativas de Millikan é dividida em três etapas, cada uma caracterizada por um método. Esses métodos foram enumerados por Holton como Método I (essencialmente o método de Wilson), Método II (gota d’água isolada com alto campo elétrico) e Método III (gota de óleo).
Com o Método I eles obtiveram, para a carga do elétron, uma relação formalmente idêntica à de Thomson-Wilson, com valor médio em torno de 1.3x10-19 coulomb. Uma fonte de erro muito importante nos métodos baseados na câmara de bolhas foi destacada por Rutherford, segundo o qual, a dificuldade de se levar em consideração o efeito da evaporação das gotículas de água resultava em valores superestimados para o número de gotículas e, conseqüentemente, em valores subestimados para a carga do elétron. Portanto, o problema crucial era reduzir o efeito da evaporação. A idéia imediata de Millikan foi utilizar um forte campo elétrico (obtido com uma tensão da ordem de 10 kV) para imobilizar a camada superior da nuvem de gotículas ionizadas e com isso acompanhar seu processo de evaporação. Qual não foi sua surpresa quando, ao ligar a bateria, a nuvem se dissipou completa e imediatamente, ao invés de ficar imobilizada como ele estava esperando! Observações sucessivas levaram Millikan a descobrir que depois da "explosão" da nuvem, algumas minúsculas gotículas permaneciam, proporcionando, pela primeira vez, a observação de gotas individuais; estava nascendo o Método II, na classificação de Holton. Millikan parece ter ficado extasiado com o que viu; gotas que iniciavam o movimento, depois paravam, e às vezes invertiam a direção do movimento quando o campo elétrico era desligado e depois ligado. Com a obtenção de aproximadamente 1.56x10-19 coulomb para a carga do elétron, Millikan e Begeman deveriam ficar mais do que satisfeitos. Todavia, o problema da evaporação continuava. Tentativas para resolver este problema desembocaram no experimento da gota de óleo, descrito a seguir com base no artigo de Fletcher. Para concluir essa fase do trabalho de Millikan, é muito importante destacar o fato de que, com a colaboração de Begeman, ele chegou à conclusão de que os valores das cargas das diversas gotículas eram sempre múltiplos exatos da menor carga que eles haviam obtido. Portanto, o resultado fundamental de que existe uma carga elementar, a carga do elétron, foi obtido com o Método II. Conforme veremos a seguir, o Método III, um experimento conceitualmente simples e extraordinariamente bem conduzido, ratificou a conclusão anterior, a partir de dados experimentais mais confiáveis.
O Método III e a controvérsia Millikan-Fletcher
Em setembro de 1909, Fletcher procurou Millikan para saber se ele poderia lhe sugerir algum tema de pesquisa para sua tese de doutorado. Segundo Fletcher, Millikan era um homem muito ocupado, de modo que foi muito difícil marcar uma reunião com ele. Finalmente foi marcado um encontro num dos laboratórios onde Millikan trabalhava com Begeman. Naquele momento, o principal problema a ser resolvido era o da rápida evaporação das gotículas de água. Segundo Fletcher, ao longo das discussões que eles tiveram, mercúrio, óleo, e duas ou três outras substências foram sugeridas, mas nesse tipo de discussão não é fácil ter certeza de quem sugeriu o que. De qualquer forma, ele ficou com a impressão de que ele tinha feito a sugestão, por causa da facilidade de obtenção e de manuseio do óleo. Causou-lhe surpresa o fato de que Millikan afirmou na sua autobiografia que já vinha pensando nessa solução antes de discuti-la com Fletcher e Begeman. Na verdade, Millikan escreveu que havia pensado nessa solução quando retornava da conferência do Canadá. Quer tenha sido um, ou outro o proponente, o fato, segundo Fletcher, é que Millikan teria dito que ali estava sua tese, na escolha de uma substância que não evaporasse. Em seguida ele descreve os detalhes da montagem do experimento, mas não volta a discutir a questão da substância; aparentemente os resultados obtidos com o óleo de relógio foram tão bons que eles não se dispuseram a testar outros materiais.
O equipamento usado por Millikan e Begeman era razoavelmente bem acabado, de modo que Fletcher logo percebeu que levaria algum tempo para construir um semelhante. Todavia, o grau de excitamento era tal que ele resolveu fazer uma montagem rústica. Comprou um atomizador de perfume, um pouco de óleo de relógio e iniciou sua montagem. Na primeira montagem, realizada em apenas um dia de trabalho, Fletcher borrifou gotículas de óleo diretamente sobre a abertura da placa superior do condensador; não havia a câmara (C) apresentada na figura abaixo.
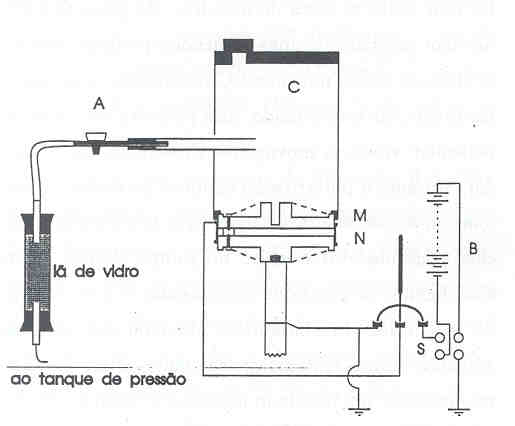
No dia seguinte, Millikan ficou muito surpreso quando soube que Fletcher tinha montado o equipamento e que este funcionava bem! Mais surpreso ficou quando, no laboratório, observou os belos fenômenos relatados acima. De acordo com Fletcher, Millikan ficou muito excitado, especialmente depois de aplicar o campo elétrico e perceber que o método seria capaz de fornecer um valor muito preciso para o valor de e. Imediatamente Millikan chamou o mecânico e encomendou uma montagem "profissional". Além dos outros componentes mostrados na montagem, foi acrescida uma fonte radioativa para aumentar a ionização das gotículas. O novo equipamento ficou pronto em uma semana, e depois de aproximadamente um mês de trabalho a imprensa já estava no laboratório em busca de informações sobre o revolucionário experimento. A publicidade foi enorme, e, na mesma medida, o excitamento de Fletcher; pela primeira vez o seu nome aparecia na imprensa, ao lado do nome de Millikan, e por várias vezes ele mostrou o experimento a personalidades importantes.
Na primavera de 1910, eles começaram a escrever um artigo para publicação. Segundo Fletcher, ele escreveu mais do que Millikan, principalmente no que se refere à modificação da lei de Stokes. Millikan contribuía principalmente fazendo correções de linguagem. Para Fletcher, aquele era um trabalho de parceria, assim como haveriam de ser os outros quatro artigos planejados. Todavia, em fins de junho, quando o artigo estava concluído, Millikan apareceu no apartamento de Fletcher, e, para sua surpresa, iniciou uma discussão genérica sobre utilização, como tese, de artigo publicado. Para Millikan, artigo usado em tese deveria ter a assinatura solitária do estudante. Fletcher logo percebeu que Millikan desejava ser o único autor do primeiro artigo: "Era óbvio que ele queria ser o único autor do primeiro artigo. Eu não queria isso, mas não via outra saída, de modo que eu concordei em usar o quinto artigo (...) como minha tese" Que Millikan estava certo do grande sucesso que adviria com a publicação daquele artigo, parece não haver dúvida; o que não se pode afirmar é que, em conseqüência disso, ele tenha planejado afastar Fletcher. Aparentemente, quando Millikan foi discutir a autoria com Fletcher, já se encontrava em andamento pelo menos a publicação de um resumo, com a sua assinatura.
Comentários finais
Os fatos, ou supostos fatos, aqui relatados constituem belo material para um exercício de especulação histórica. Para tanto, talvez seja conveniente estabelecer as relações triangulares Millikan-Begeman-Fletcher. De 1907 a setembro de 1909, Begeman trabalhou com Millikan no desenvolvimento dos Métodos I e II; em 1908, eles publicaram o primeiro artigo na Physical Review (vol. 26, p. 197) sobre resultados obtidos com o método I. Em 1910 Begeman publicou outro artigo, também na Physical Review (vol. 31, p. 45), mas, de acordo com Fletcher, ele já não trabalhava com Millikan. Por outro lado, em 9 de outubro de 1909 Millikan submete à Philosophical Magazine o primeiro trabalho sobre a gota isolada, sendo hoje considerado seu primeiro grande artigo; o segundo grande artigo foi justamente aquele publicado em Science, em 1910, o primeiro da série de artigos baseados nas medidas realizadas com Fletcher. Portanto, chama a atenção que os dois principais trabalhos de Millikan tenham sido publicados sem a participação dos respectivos estudantes, embora no texto o devido crédito seja dado aos colaboradores.
A propósito, Holton comenta que Millikan freqüentemente dava crédito à participação dos seus estudantes nos experimentos, e que as anotações nos cadernos do laboratório nem sempre eram de Millikan. Nesse sentido, seria interessante ter acesso aos cadernos de 1909, para verificar as etapas iniciais da montagem do equipamento, bem como o uso do óleo e outras substâncias. Infelizmente esses cadernos desapareceram!
BIBLIOGRAFIA
- ANDERSON, D.L. The Discovery of the Electron, Princeton: D. Van Nostrand Company, (1964). p. 77-100.
- BASSALO, J.M.F. Crônicas da Física. Tomo 1 (1987), Tomo 2 (1990), Tomo 3 (1992), Tomo 4 (1994), Editora Universitária UFPA, Belém.
- DOS SANTOS, C.A. A participação de Fletcher no experimento da gota de óleo de Millikan. Revista Brasileira de Ensino de Física, 17 (1), 107-116 (1995).
- EPSTEIN, P.S. Rev. Mod. Phys. 20, 10-25 (1948).
- FLETCHER, H. Phys.Today, 35, 43-47, June (1982).
- GARDNER, M.B. Phys. Today, 34, 116, Oct (1981).
- HOLTON, G. The Scientific Imagination: Case Studies, Cambridge: Cambridge University Press, (1978). p. 39.
- KARGON, R.H. The rise of Robert Millikan, Ithaca: Cornell University Press, (1982). p.11.
- KUNRATH, J.I. Experiências que abalaram afísicaclássica, Porto Alegre: Instituto de Física da UFRGS (1993). Trata-se de uma série de roteiros para a disciplina Laboratório Avançado I, com breves revisões históricas.
- MILLIKAN, R.A. Phys. Rev. 8, 595-625 (1916).
- MILLIKAN, R.A. Phys. Rev. 7, 355-388 (1916).
- ROMER, A. The Phys. Teacher, 16, 78-85 (1978).
- SEGRÈ, E. From X-rays to quarks, New York: Freeman and Company, (1980). p. 190).
- ZUCKERMAN, H. Scientific elite, New York: The Free Press, (1977). p. 101
Decomposição da luz solar com um prisma, realizada por Newton
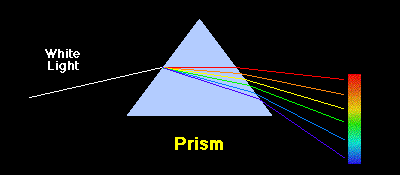
O experimento da decomposição da luz solar, realizada por Newton, é extraordinariamente simples. Um prisma de vidro é suficiente. Como ilustra a figura abaixo, ao passar por um prisma, a luz solar, que é branca, se decompõe nas cores do arco-íris.
No caso do arco-íris, são as gotículas de água que fazem o papel do prisma.
 |
 |
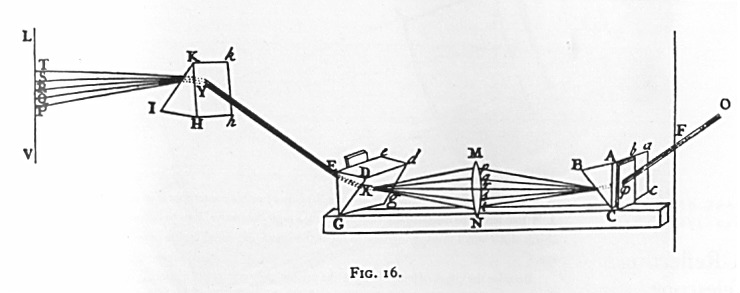
Newton demonstrou que combinando adequadamente dois ou mais prismas, é possível decompor e recompor a luz branca. A separação é possível porque cada cor tem um índice de refração diferente. Isto é, apresenta um desvio diferente quando passa de um meio (ar) para outro (vidro).
Bibliografia
- EISBERG, R.M., LERNER, L.S. Física. Fundamentos e Aplicações, v.4. São Paulo: McGraw-Hill (1983).
- HALLIDAY, D., RESNICK, R. Fundamentos de Física, v. 4.. Rio de Janeiro: Livros Técnicos e Científicos (1991).
- SEARS, F., ZEMANSKY, M.W., YOUNG, H.D. Física, v.4. Rio de Janeiro: Livros Técnicos e Científicos (1985).
Experimento com a balança de torsão, realizada por Cavendish
Por volta de 1686, Isaac Newton chegou à conclusão que o movimento dos planetas e da lua, bem como dos corpos em queda livre, como uma maçã, poderia ser explicado pela sua lei da gravitação universal, cuja fórmula é
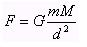
Nesta equação, m e M representam as massas dos corpos, enquanto d representa a distância entre elas. G é uma constante, conhecida como constante gravitacional. Muita gente conhece a lei pela sua expressão literal: os corpos se atraem na razão direta dos produtos das suas massas e na razão inversa do quadrado da distância entre eles. É provável que Newton tenha estimado o valor de G a partir da aceleração gravitacional de corpos em queda livre.
Em 1797 (um século depois da lei de Newton), Henry Cavendish iniciou seus experimentos com a balança de torsão. Embora a história tenha consagrado seu nome em referência a este experimento, ele não foi o pioneiro. De acordo com Laurent Hodge, Cavendish credita John Michell pelo desenvolvimento do projeto. Não se sabe a data exata em que Michell construiu sua balança. No seu artigo, Cavendish (1798) diz que o projeto de Michell teve início "muitos anos atrás", mas ele não pôde concluí-lo antes da sua morte (1793). Numa nota de rodapé, Cavendish afirma que Michell havia-lhe descrito o equipamento antes de 1785, ano em que Charles Augustus Coulomb desenvolveu um equipamento similar para determinar sua famosa lei de interação entre cargas elétricas.
Portanto, não se sabe quem foi o pioneiro na invenção da balança de torsão. Costuma-se creditar Michell e Coulomb.
A balança de torsão
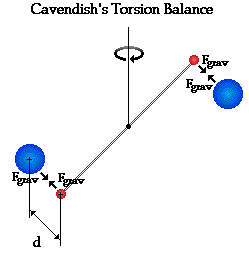
| O esquema na figura ao lado foi extraído do excelente site
The Physics Classroom and Mathsoft Engineering & Education, Inc..
Duas pequenas massas são fixadas nas pontas de uma barra suspensa por um fio. Essas pequenas massas podem se deslocar. Duas outras massas (bolas maiores) são mantidas fixas nas proximidades das massas menores. Inicialmente, a distância entre as massas é d. A força de interação gravitacional provocará um deslocamento da massa menor em direção à massa maior. Este deslocamento causará uma torsão no fio que sustenta a barra. A medida do ângulo de torsão permite a determinação da constante da gravitação universal (G), presente na lei da gravitação universal de Newton (veja equação acima). |
 |
Bibliografia
- "'BICENTENARY of the CAVENDISCH EXPERIMENT' CONFERENCE", acessado em 7/dez/2002, em http://www.phys.lsu.edu/mog/mog13/node11.html
- FEYNMAN, R.P., LEIGHTON, R.B., SANDS, M. The Feynman lectures on physics, v. 1. Addison-Wesley (1969).
- HALLIDAY, D., RESNICK, R. Fundamentos de Física, v. 2. Ótica e Física Moderna. Rio de Janeiro: Livros Técnicos e Científicos (1991).
- HODGES, L., "The Michell-Cavendish experiment", acessado em 7/dez/2002, em http://www.public.iastate.edu/~physics_221/Michell.htm
- SAETA, P.N. "The Cavendish Experiment", acessado em 7/dez/2002, em http://kossi.physics.hmc.edu/Courses/p23a/Experiments/Cavendish.html
- "THE CONTROVERSY over NEWTON'S GRAVITATIONAL CONSTANT", acessado em 7/dez/2002, em http://www.npl.washington.edu/eotwash/gconst.html
- THE PHYSICS CLASSROOM and MATHSOFT ENGINEERING & EDUCATION, Inc., "Lesson 3: Universal Gravitation", acessado em 7/dez/2002, em http://www.physicsclassroom.com/Class/circles/U6L3d.html
Medida da circunferência da terra, realizada por Eratóstenes
A figura abaixo, extraída do site de Dennis P. Donovan, ilustra a engenhosa solução encontrada por Eratóstenes.
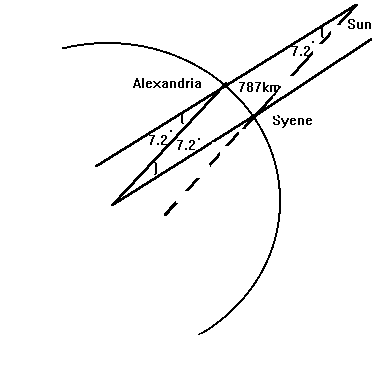
Eratóstenes, um geógrafo Grego (276-194 BC), sabia que durante o solstício do verão, os raios solares atingiam perpendicularmente a superfície de Siena (Egito) ao meio-dia. Neste mesmo instante, a inclinação dos raios solares era de 7,2° em Alexandria. Sabendo que os raios solares chegam à terra paralelamente, e que a distância entre Siena e Alexandria é 787 km, Eratóstenes usou uma simples regra de três para calcular o perímetro da terra. Isto é
Portanto, a circunferência da terra será X = 39350 km. Para se calcular o raio da terra, basta fazer X=2pR
Espalhamento de Rutherford
O nono experimento mais belo da física é o espalhamento de partículas alfa, observado por Ernest Rutherford quando ele fez incidir um feixe dessas partículas sobre uma folha de ouro. A figura abaixo, extraída do site menloschool, ilustra o arranjo experimental.
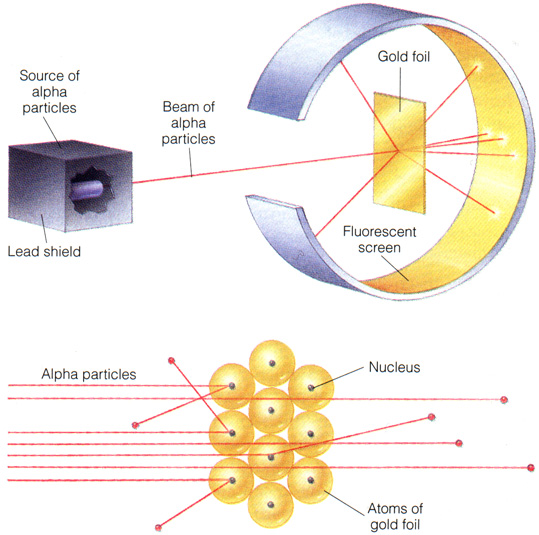
A surpresa do experimento foi que, ao invés de sofrerem pequenos desvios, muitas partículas apresentaram grandes desvios. Algumas até foram retroespalhadas. Mal comparando, é como se uma bala de revolver retornasse ao ser atirada contra uma folha de papel.
O resultado motivou Rutherford a propor, por volta de 1911, um modelo atômico alternativo ao de Thomson, até então considerado válido. O modelo de Thomson era conhecido como modelo do pudim de ameixa, porque consistia numa mistura de cargas positivas e negativas. As cargas negativas, o próprio Thomson havia descoberto em 1897, eram os elétrons, mas nada se sabia sobre a identidade das cargas positivas.
Rutherford propôs um modelo planetário, com um centro muito pequeno, onde se concentrava toda a carga positiva e praticamente toda a massa do átomo, em torno do qual orbitavam os elétrons. Esta idéia foi posteriormente desenvolvida por Bohr e resultou no que hoje se conhece como modelo de Bohr
O Pêndulo de Foucault
Em 1600, Giordano Bruno foi condenado à fogueira pela Inquisição porque acreditava que a terra se movia em torno do seu eixo e em torno do sol. Trinta e três anos depois, Galileu Galilei só não teve o mesmo destino porque renunciou à sua convicção científica.
A dificuldade em confirmar a rotação da terra reside no fato de que se trata de uma rotação muito lenta (0,0007 rotações por minuto). Em 1851, o astrônomo francês Jean Bernard Leon Foucault realizou uma bela e simples experiência capaz de demonstrar a rotação da terra. Com uma corda de 67 metros, fixa no teto do Panteon de Paris, ele suspendeu uma esfera de ferro de 28 kg e imprimiu-lhe um movimento pendular.

Na seqüência, o plano do pêndulo passou a apresentar uma lenta rotação no sentido horário. Este movimento foi facilmente explicado a partir da suposição de que a terra gira em torno de seu eixo.
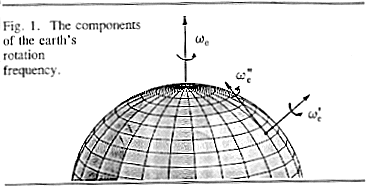
Este experimento ficou mais conhecido pelo nome do dispositivo usado, isto é, pelo pêndulo de Foucault, tendo sido considerado, pelos leitores da revista Physics World, o décimo mais belo experimento da física.
Agradecimentos
Aos sites da uoguelph e da unsw, pelo uso das figuras acima.
Para saber mais:
Movimento de um pendulo no polo sul.
| |
|
|