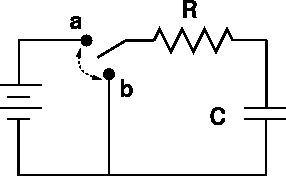
Introdução

 

Um circuito é chamado de circuito RC quando ele consiste em um capacitor, um resistor e uma bateria, ligados em série. Um capacitor pode armazenar energia e um resistor em série modifica o tempo que o capacitor carrega ou descarrega.

 

 

 

Essa relação entre resistência e capacitância é a constante de tempo capacitiva do circuito e é representada pelo símbolo t , que é definida pelo produto dos seus respectivos valores, visto que:

t = Ohm x Farad = [(Volt x Segundo) / Coulomb] x (Coulomb / Volt) = Segundo

Fechando o circuito com a chave em a, o circuito com a bateria, o resistor e o capacitor é completo. Percorrendo pelo sentido horário a partir da bateria aplicando as regras das malhas, temos que:

e – (iR) – (q/C) = 0

Como dq/dt = i, encontramos uma equação diferencial:

 

R(dq/dt) + q/C = e

A solução desta equação diferencial é :

q = Ce (1 – exp(-t/RC))

Derivando a corrente em relação ao tempo:

i = (e /R)exp(-t/RC).

Podemos também medir o potencial sabendo que V = q/C. Então, temos que:

V = e (1 – exp(-t/RC))

Utilizando t = RC na equação da carga, temos que q = Ce (1 – exp(-1)) = 0.63Ce , ou seja, durante uma constante de tempo RC (t ), o capacitor carrega aproximadamente 63% da carga possível.

 

Fechando a chave em b, montamos um circuito com o resistor e o capacitor. Pela regra das malhas, temos que:

R(dq/dt) + q/C = 0

A solução desta equação diferencial é:

q = qoexp(-t/RC)

onde qo é a carga do capacitor no momento em que se troca a chave de a para b.

Derivando:

i = (qo/RC)exp(-t/RC).

Sabendo que V = q/C, tiramos uma equação para V:

V = (qo/C)exp(-t/RC)

Quando completamente carregado, o capacitor possui carga igual a e C, portanto
qo/C é igual a e , reduzindo a equação para:

V = e exp(-t/RC)