
As estrelas visíveis no céu noturno variam com a época do ano, a hora do dia e com a latitude do observador.
A dependência com a época do ano, é causada pelo fato de o Sol se mover com relação às estrelas, ao longo do ano. Este movimento anual do Sol , como veremos mais adiante, é o resultado do movimento orbital da Terra em torno do Sol. O caminho do Sol no céu em seu movimento anual se chama eclítica . Dessa forma, as estrelas que aparecem no céu noturno, ou seja, que estão longe da posição do Sol na esfera celeste, mudam lentamente ao longo do ano. O fato do Sol mover-se por entre as estrelas (fixas) sobre a eclítica também tem conseqüências sobre a marcação do tempo, pois faz com que o dia solar (baseado no movimento diurno do Sol) tenha duração diferente do dia sideral (baseado no movimento diurno do ponto γ). Nos capítulos sobre sistemas de tempo veremos isso em mais detalhe, mostrando a relação e as fórmulas de conversão entre hora solar e sideral.
A dependência com a hora do dia se deve à rotação da Terra. De maneira geral, os astros nascem e se põem no céu à medida em que a Terra gira em torno de seu eixo. Como esse movimento faz com que um observador fixo na superfície da Terra descreva um círculo no espaço, os astros, vistos por este observador, descrevem também um círculo na esfera celeste. A este movimento chamamos de movimento diurno. A rotação se dá de oeste para leste; logo, o movimento diurno dos astros no céu se dá no sentido inverso, de leste para oeste. O movimento de um ponto fixo na superfície da Terra é paralelo ao equador, mantendo-se constante, portanto, a latitude do ponto. Da mesma forma, o círculo descrito por uma estrela em seu movimento diurno é paralelo ao equador celeste. Portanto, não se altera a declinação δ da mesma (ou a sua distância polar p). Como o ponto γ é fixo com relação às estrelas (pelo menos durante um dia), também ele se move no céu ao longo do dia. A ascensão reta então é mantida constante. Essa é a grande vantagem das coordenadas equatoriais sobre as horizontais: enquanto a altura h e o azimute A de um astro variam ao longo do dia, devido ao movimento diurno, a ascensão reta α e declinação δ são fixas. Essas últimas variam apenas em escalas de tempo muito mais longas, devido aos efeitos de precessão, nutação, aberração, paralaxe e movimento próprio, que veremos em maior detalhe mais adiante.
Em geral, parte do círculo descrito por um astro no céu ao longo de um dia, estará acima do horizonte do observador e parte dele estará abaixo. No instante em que o astro está no plano que contém o meridiano astronômico do observador, sua altura no céu é um extremo. Isso acontece duas vezes em um dia sideral; na culminação superior (ângulo horário H = 0°) a altura do astro é máxima, na culminação inferior (H = 180°) sua altura é mínima. A culminação superior é a melhor ocasião para se observar o astro, já que sua altura h é máxima (distância zenital, zmin, é mínima). Neste instante de passagem meridiana, podemos também estabelecer relações simples envolvendo a altura hmax, a declinação δ da estrela e a latitude φ do observador. O primeiro passo para isso é o de construir o diagrama do plano meridiano do observador . Este é mostrado na figura abaixo. Nele vemos o observador em O, sua vertical OZ que encontra a esfera celeste no zênite (Z) e os pontos cardeais norte (N) e sul (S). Também pertencem ao plano meridiano o pólo celeste elevado (no caso da figura é o pólo celeste sul, PSC) e um ponto do equador celeste que cruza o plano meridiano em EC. O meridiano astronômico é representado pelo semi-círculo no diagrama. A posição de uma estrela que faz sua culminação superior também é mostrada, juntamente com sua declinação δ e sua distância zenital z. Como latitudes e declinações a sul são arbitradas como de valor negativo, enquanto que altura acima do horizonte e distância zenital são sempre positivas, faz-se necessário incluir um sinal negativo na frente de alguns ângulos mostrados, como forma de compatibilizar estas definições.

Note que a figura mostra um resultado muito importante: a altura do pólo elevado é numericamente igual à latitude do observador . Para nos convercermos disso fazemos uso da próxima figura, em que vemos o plano meridiano de um observador situado no ponto O da superfície da Terra. Nesta figura, vemos não apenas o plano meridiano, mas também todos os pontos na superfície da Terra que compartilham deste plano, incluindo-se ainda o centro da Terra e os seus pólos norte e sul geográficos (PNG e PSG, respectivamente). É fácil provar, usando equivalência de ângulos correspondentes e lembrando que o eixo de rotação é perpendicular ao equador e que a vertical do observador é perpendicular à sua horizontal, que a altura do pólo celeste elevado é, de fato, numericamente igual à latitude.

Vejamos a figura em detalhe. A reta O-EC no diagrama do plano meridiano (que agora está de cabeça para baixo) é paralela ao equador da Terra, por definição de Equador Celeste. O mesmo se aplica à direção O-PSC: por definição, a direção ao pólo celeste é paralela ao eixo de rotação. Logo, O-EC é perpendicular a O-PSC. O ângulo entre as direções C-O-Z (vertical do observador em O) e O-EC corresponde ao ângulo de inclinação do Equador Celeste com relação à vertical do observador. Este ângulo, por equivalência de ângulos formados por uma transversal cortada por duas paralelas, é igual ao módulo da latitude φ (nesse caso, -φ) do observador O. O ângulo entre as direções C-O-Z e O-PSC corresponde à distância zenital do pólo celeste PSC. Eles será o complemento da inclinação de EC (= 90° + φ). E a altura do pólo PSC (ângulo entre a horizontal do observador, direção S-O-N, e a direção O-PSC), usando novamente a complementariedade, é -φ. Como queríamos demonstrar!
Voltemos agora à questão fundamental da relação matemática envolvendo a altura hmax e a declinação δ da estrela e a latitude φ do observador. São duas as relações envolvendo estas variáveis no instante da passagem meridiana. A relação a ser usada depende da culminação superior se dar a norte (A = 0°) ou a sul de zênite (A = 180°):
φ = δ - zmin (se A = 0°)
φ = δ + zmin (se A = 180°)
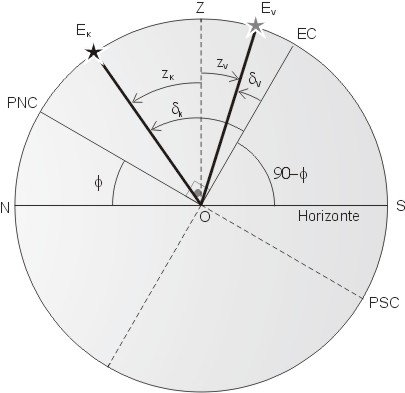
Essas duas fórmulas podem ser facilmente deduzidas pela figura abaixo, que mostra novamente o diagrama do plano meridiano. Note que o pólo celeste elevado agora é o pólo celeste norte, PNC. O ponto do equador celeste que cruza o plano meridiano é novamente marcado como EC. Como agora a latitude é positiva, a altura do pólo elevado, PNC, é simplesmente igual a φ. A distância zenital do ponto EC tem também o mesmo valor.
A figura mostra a situação de culminação superior de duas estrelas, uma a norte do zênite (K) e a outra a sul (V). Vemos então pela distância zenital de EC que:
φ = δk - zk (Ak = 0°)
φ = δv + zv (Av = 180°)
Consideremos agora o efeito da latitude do observador sobre a visibilidade das estrelas. Estrelas muito próximas do pólo norte celeste, por exemplo, estão sempre acima (abaixo) do horizonte de observadores situados em latitudes norte (sul). Estrelas sempre acima do horizonte são chamadas de circumpolares. Estrelas sempre abaixo do horizonte de um observador são simplesmente chamadas de invisíveis. Para que uma estrela seja circumpolar, a altura mínima que ela atinge durante todo o dia tem que ser positiva, ou seja, hmin > 0°. A altura mínima de qualquer astro ocorre na sua culminação inferior. Pela figura abaixo, que mostra novamente o diagrama do plano meridiano, podemos ver que a condição de circumpolaridade de uma estrela para um observador no hemisfério norte é dada por:
δ > 90°- φ.
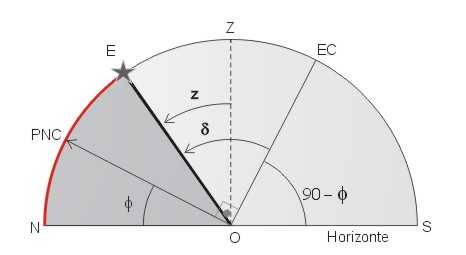
Vejamos isso em mais detalhe: o semi-círculo que passa pelos pontos cardeais norte (N) e sul (S) e também pelo zênite é obviamente o meridiano astronômico do observador. O pólo celeste elevado é o pólo celeste norte (PNC), cuja direção é perpendicular ao equador celeste. Este último cruza o meridiano do observador no ponto EC, como nas figuras anteriores. A altura do pólo celeste visível é igual à latitude do observador, sendo que a direção de PNC é bissetriz do arco do meridiano astronômico mostrado em tonalidade escura na figura. Este arco representa a zona ocupada pelas estrelas circumpolares para o observador em questão. Logo as estrelas circumpolares terão distância polar p < φ. Mas p = 90° - δ. Logo 90° - δ < φ, o que resulta na condição de circumpolaridade dada acima, se resolvermos esta inequação para a declinação.
Podemos determinar nossa latitude pela observação do movimento diurno de estrelas circumpolares. O método é ilustrado na figura abaixo.

Nela vemos novamente uma representação do plano meridiano de um observador. Vemos o pólo elevado (PNC), de altura igual à latitude φ do observador. Vemos também as posições de uma estrela circumpolar nos momentos da culminação superior (C.S.) e inferior (C.I.). Como a declinação da estrela não muda ao longo de um dia, sua distância polar p também se mantém constante, e é mostrada também na figura. Assim, podemos ver facilmente pela figura que as alturas máxima (hs) e mínima (hi) da estrela durante seu movimento diurno podem ser expressas em função de φ e p:
hi = φ - p
hs = φ + p
Logo, eliminando p do sistema de equações acima, teremos:
φ = (hs + hi) / 2
Para um observador no Hemisfério Sul da Terra, a fórmula é praticamente a mesma. A única diferença é que temos que lembrar que, neste caso, convenciona-se que a latitude é negativa, enquanto que as alturas de uma estrela circumpolar serão sempre positivas. Assim temos apenas que mudar um sinal algébrico:
φ = - (hs + hi) / 2
Note que o pólo sul celeste está sempre abaixo do horizonte do observador em questão. Estrelas suficientemente próximas a ele estarão sempre invisíveis a este observador. A condição para uma estrela nunca nasça (seja invisível) é (hmax < 0°):
δ < -(90°-φ)
Podemos confirmar isso na figura abaixo, onde novamente mostramos o diagrama do plano meridiano de um observador de latitude positiva. Mostramos também o ângulo δmin, que é o ângulo mínimo que uma estrela tem que formar com o equador celeste, para que ela não suba acima do horizonte. É fácil ver que este ângulo é numericamente igual a (90°-φ). A declinação desta estrela, necessariamente negativa, será δ = -δmin = -(90°-φ). Apenas declinação mais próximas do pólo sul celeste PSC (ou seja, mais negativas ainda) corresponderão às estrelas invisíveis. Daí resulta a condição dada acima.

Por exemplo, no caso de um observador cuja latitude é φ = 45°, estrelas com δ > 45° são circumpolares e estrelas com δ < -45° são invisíveis. Se φ = 60°, as estrelas circumpolares terão δ > 90° - φ = 30° e as invisíveis estarão na região δ < -(90° - φ) = -30°
As condições de circumpolaridade e invisibilidade dadas acima se aplicam para o caso em que o observador está no hemisfério norte da Terra (ou seja, φ > 0°). Para o hemisfério sul (φ < 0°) teremos:
Circumpolaridade: δ < -(90° + φ)
Invisibilidade: δ > (90° + φ)
Tente desenhar diagramas do plano meridiano de um observador, semelhantes aos diagramas acima, mas para o caso de um observador no hemisfério sul terrestre. Ao desenhá-los, lembrando das definições de pólo e equador celestes e lembrando que a altura do pólo sul celeste será sempre igual ao módulo da latitude do observador, você deverá ser capaz de deduzir as expressões acima.
Basilio Santiago, santiago@if.ufrgs.br