Métodos Computacionais no Ensino da Física

3.2 Problema exemplo

Como foi feito no caso da planilha, será utilizado, como ilustração na apresentação do Modellus, um assunto específico de física. Um dos destaques do software é que ele permite montar animações, o que é particularmente interessante quando o assunto é mecânica. Portanto, será escolhido um tema nesta área: o tradicional movimento do projétil.

Desprezando-se o arraste do ar, este movimento resulta da combinação de um movimento uniforme horizontal com um movimento uniformemente variado vertical. Portanto, é possível resolver as equações e escrever as variações das posições (horizontal e vertical) como funções do tempo (as assim chamadas "equações horárias"). Ou ainda, pode-se fornecer ao software as soluções do problema na forma algébrica. É o que será feito nesta aula. O software então serve para obter valores numéricos, produzir gráficos e tabelas, e visualizar o movimento numa animação.

Na presença de arraste aerodinâmico, a situação fica mais complicada. A segunda lei de Newton fornece as equações fundamentais do movimento, mas mesmo se for adotado um modelo para a força de arraste, será difícil resolvê-las, pois a força certamente não será constante; será função da velocidade. Aí entra em jogo um recurso muito potente do Modellus: ele sabe resolver (numericamente) as equações. Isto será o tema da próxima aula.

Supõe-se que o projétil é lançado (no instante t=0) com uma velocidade inicial de módulo v₀, fazendo um ângulo θ₀ com a horizontal.

Será conveniente utilizar um sistema de eixos tais que o eixo Ox seja horizontal e o eixo Oy vertical, orientado para cima. Colocar-se-á a origem do sistema de eixos no ponto de lançamento (x=y=0).

Na ausência de arraste do ar, a única força aplicada ao corpo é a força gravitacional, que atua verticalmente para baixo. Não há força atuando na horizontal e o movimento nesta direção é uniforme. Como mostra a Figura 3.2.1, a componente horizontal da velocidade inicial é v₀ cos(θ₀). Portanto, o movimento horizontal é descrito pelas equações

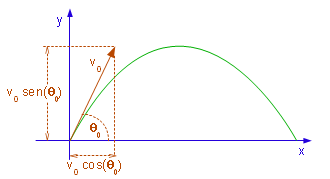
Na vertical, atua a força gravitacional, que produz uma aceleração de módulo g=9,8m/s². Vale notar que, ao fazer esta suposição, excluí-se movimentos cujos alcances horizontal e/ou vertical, não sejam muito pequenos em comparação com o raio da Terra. Nestas condições, o movimento vertical é uniformemente variado, com aceleração -g. Já que a componente vertical da velocidade inicial é v₀ sen(θ₀) [veja a Figura 3.2.1], o movimento vertical é então descrito pelas equações

Será interessante ter à mão as expressões de algumas quantidades que caracterizam o movimento, em especial o tempo de vôo T (até o projétil voltar à altura do ponto de lançamento) e o alcance A (a distância horizontal percorrida até este instante). Pode-se deduzir o tempo de vôo da condição y=0 que, dada a Equação 3.2.4, pode ser escrita na forma

A primeira solução desta equação (t=0) corresponde evidentemente ao instante de lançamento. A outra fornece o tempo de vôo: Substituindo-se este tempo na Equação 3.2.2, obtém-se a expressão do alcance: onde foi utilizada uma relação trigonométrica bem conhecida.

Outro aspecto do movimento que se deseja estudar é a variação com o tempo das energias cinética, potencial e mecânica total. Sendo m a massa do projétil, a energia cinética é

e a energia potencial (gravitacional) é Como é sabido, na ausência de arraste, a energia mecânica total deve se conservar.

Pode-se, agora, estudar esse sistema com Modellus!